条件が複数ある複雑な2経路を作成したい

Question

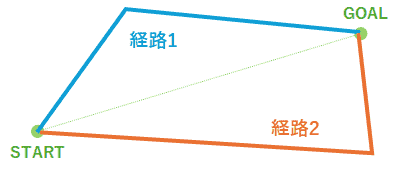
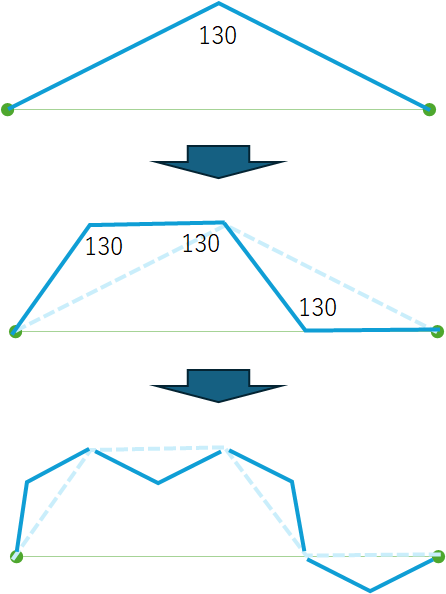
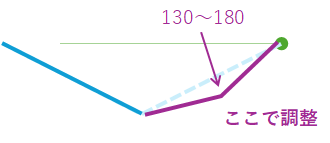
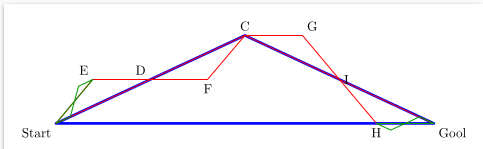
### 実現したいこと以下の条件を満たす2経路を作成して図示したいです。以下の絶対条件を満たせば、どのような経路を通っても可とします。【経路の絶対条件】 1. 経路1と経路2は必ず指定された経路長になること 2. STARTとGOALは必ず指定された座標位置で固定されていること　　例）経路1：START (0,0)、GOAL (10,10) 　　　　経路2：START (0,1)、GOAL (10,15) 3. 1つの経路における各点のx座標は、前の点のx座標から0以上となっていること　　例) 経路1：m(n)のx座標 ≦ m(n+1)のx座標 4. 経路1と経路2は交わらず、かつ距離が〇以上離れていること（〇の値は任意で変更可能） 5. 1つの経路内で発生する角度は全て130°≦θ≦180°となること　　例) 経路1：m(n-1)とm(n)を結ぶ線分Aと、m(n)とm(n+1)を結ぶ線分Bのなす角が130°≦θ≦180° ※補足※ 目的としましては、START/GOALの座標及び経路長が場合によって変更になるため、変更になった際に条件を満たす経路を1つ作成することを目的としています。そのため、確実に条件を満たす経路が1つ作成されればそれでOKとなります。（乱数で複数のパターンの経路を作成する必要はありません。） ### 発生している問題・分からないこと LLMを使用してソースコードを作成していますが、以下のような問題が発生しなかなか実現できません。 ※LLMで作成しているためソースコードもおかしな部分や無駄な部分があるかもしれません。 - 最適解が導出されない（収束しない）　→現在は収束しない場合に"条件を満たす経路が見つかりませんでした。"と表示するようにしているのですが、可能であれば一か八かではなく、100%最適解が導出されるようにしたいです。 - 実行時間が長すぎる　→最適解が可能な限り導出されるようにプログラムを変更すると、とんでもなく実行時間が長くなってしまいます。（1時間以上かかり、それでも最適解が導出されないことがあります。）　　現在のプログラムではおそらく難しいのかと思いますが、可能であれば実行時間を短くしたいです。 - 条件を満たさない場合がある　→実行時間を短くしようとしてLLMに相談すると、どうしても条件が厳しいようで条件を緩和しようとします。（特に4と5の条件を一度に満たすのが難しいようです。）　　ただ絶対条件を満たさなければ意味がないので、条件を緩和するのは難しい状況です。 ※ソースコードが非常に長いですがご容赦ください。 ### 該当のソースコード ```Python import numpy as np import matplotlib.pyplot as plt starts = [ np.array([0, 0]), np.array([0, 1]), ] goals = [ np.array([10, 10]), np.array([10, 15]), ] target_lengths = [40, 40] num_points = 15 def calculate_length(points): return np.sum(np.linalg.norm(points[1:] - points[:-1], axis=1)) def generate_monotonic_x(start, goal, num_points): total_dx = goal[0] - start[0] dxs = np.random.rand(num_points + 1) dxs = dxs / dxs.sum() * total_dx x_points = np.cumsum(dxs) + start[0] x_points = x_points[:-1] return x_points def check_angle_constraint(points, start, goal, min_angle_deg=130): path = np.vstack([start, points, goal]) min_cos = np.cos(np.deg2rad(180-min_angle_deg)) for i in range(1, len(path)-1): v1 = path[i] - path[i-1] v2 = path[i+1] - path[i] norm1 = np.linalg.norm(v1) norm2 = np.linalg.norm(v2) if norm1 < 1e-8 or norm2 < 1e-8: return False cos_theta = np.dot(v1, v2) / (norm1 * norm2) if cos_theta ＜ min_cos: return False return True def check_all_constraints(points1, points2, starts, goals): # x座標一致 if not np.allclose(points1[:,0], points2[:,0]): return False # y2 > y1+1 if not np.all(points2[:,1] > points1[:,1] + 1.0): return False # x座標単調増加 if not (np.all(np.diff(points1[:,0]) > 0) and np.all(np.diff(points2[:,0]) > 0)): return False # 角度制約 if not (check_angle_constraint(points1, starts[0], goals[0], min_angle_deg=130) and check_angle_constraint(points2, starts[1], goals[1], min_angle_deg=130)): return False return True def generate_y_seq_with_constraints(x_points, start_y, goal_y, num_points, amplitude=0.5, min_angle_deg=130): # 逐次生成で角度制約を満たすy座標列 y_seq = np.linspace(start_y, goal_y, num_points+2)[1:-1] y_points = [] for i in range(num_points): for _ in range(100): y = y_seq[i] + np.random.randn() * amplitude tmp_points = np.array(y_points + [y]) tmp_x = x_points[:i+1] tmp_pts = np.stack([tmp_x, tmp_points], axis=1) if i < 2: y_points.append(y) break else: if check_angle_constraint(tmp_pts, np.array([x_points[0], start_y]), np.array([x_points[i], goal_y]), min_angle_deg=min_angle_deg): y_points.append(y) break else: # 失敗したら再生成 return None return np.array(y_points) max_trials = 10000 for trial in range(max_trials): # x座標生成 x_points = generate_monotonic_x(starts[0], goals[0], num_points) # y1生成（角度制約を満たすまで逐次生成） for y1_trial in range(100): y1_points = generate_y_seq_with_constraints(x_points, starts[0][1], goals[0][1], num_points, amplitude=0.5, min_angle_deg=130) if y1_points is not None: break else: continue # y2生成（y1より十分大きく、角度制約を満たすまで逐次生成） for y2_trial in range(100): margin = 2.0 amplitude2 = 0.5 y2_base = y1_points + margin y2_points = [] for i in range(num_points): for _ in range(100): y = y2_base[i] + np.abs(np.random.randn() * amplitude2) tmp_points = np.array(y2_points + [y]) tmp_x = x_points[:i+1] tmp_pts = np.stack([tmp_x, tmp_points], axis=1) if i < 2: y2_points.append(y) break else: if check_angle_constraint(tmp_pts, np.array([x_points[0], starts[1][1]]), np.array([x_points[i], goals[1][1]]), min_angle_deg=130): y2_points.append(y) break else: break if len(y2_points) == num_points and np.all(np.array(y2_points) > y1_points + 1.0): break else: continue points1 = np.stack([x_points, y1_points], axis=1) points2 = np.stack([x_points, np.array(y2_points)], axis=1) # 経路長微調整 for adjust_trial in range(100): # 経路長計算 path1 = np.vstack([starts[0], points1, goals[0]]) path2 = np.vstack([starts[1], points2, goals[1]]) len1 = calculate_length(path1) len2 = calculate_length(path2) # 長さ調整 diff1 = target_lengths[0] - len1 diff2 = target_lengths[1] - len2 # y座標に均等分配 points1[:,1] += diff1 / num_points points2[:,1] += diff2 / num_points # 制約再チェック if check_all_constraints(points1, points2, starts, goals): # 最終チェック path1 = np.vstack([starts[0], points1, goals[0]]) path2 = np.vstack([starts[1], points2, goals[1]]) if (abs(calculate_length(path1) - target_lengths[0]) < 1e-6 and abs(calculate_length(path2) - target_lengths[1]) < 1e-6): break else: continue # すべて満たしたら終了 break else: print("条件を満たす経路が見つかりませんでした。") path1 = np.vstack([starts[0], points1, goals[0]]) path2 = np.vstack([starts[1], points2, goals[1]]) print(f'経路1の長さ: {calculate_length(path1):.8f}') print(f'経路2の長さ: {calculate_length(path2):.8f}') print(f'全ての中間点でx座標一致: {np.allclose(points1[:,0], points2[:,0])}') print(f'全ての中間点でy2>y1+1: {np.all(points2[:,1] > points1[:,1] + 1.0)}') print(f'経路1なす角制約: {check_angle_constraint(points1, starts[0], goals[0], min_angle_deg=130)}') print(f'経路2なす角制約: {check_angle_constraint(points2, starts[1], goals[1], min_angle_deg=130)}') plt.plot(path1[:, 0], path1[:, 1], marker='o', label='Path 1') plt.plot(path2[:, 0], path2[:, 1], marker='o', label='Path 2') plt.plot(starts[0][0], starts[0][1], 'ro') plt.plot(goals[0][0], goals[0][1], 'go') plt.plot(starts[1][0], starts[1][1], 'ro') plt.plot(goals[1][0], goals[1][1], 'go') plt.title('Paths with All Constraints') plt.xlabel('X-axis') plt.ylabel('Y-axis') plt.legend() plt.grid() plt.show() ``` ### 試したこと・調べたこと - [x] teratailやGoogle等で検索した - [x] ソースコードを自分なりに変更した - [ ] 知人に聞いた - [ ] その他 ##### 上記の詳細・結果 LLMに質問したり、自分で様々なアルゴリズム等を調べて変更をかけていますが、未だに上記の課題を解決できていません。 ### 補足自分がアルゴリズム等にあまり明るくないため、このようなアルゴリズムが良い等のアドバイスがありましたらぜひ教えてください。また自分が少しばかりPythonに触れていたため、現在はPythonでプログラムを作成していますが、Python以外の言語の方が実現可能性がより高い等のアドバイスがありましたら、他の言語を使用することも考えています。（特に実行時間の面では他の言語の方が有効かもしれません。）他にもAIを使用する方が実現可能性が高い等ありましたら、AIに関しても勉強しようと考えています。（AIに関してはほとんど知識が無い状態です。）もし何かアドバイス等ございましたらぜひご意見をお願いいたします。

Answer

この回答一部撤回
「解がない場合もあるよね」が間違いかもしれない。
三角形を折りたたむことしか頭になかった。
fanaさんの追記の「ここで調整」みたく膨らまさせるという手がありますね

SGを底とする頂角130度以下の二等辺三角形で 所定の長さが稼げればそのまま解ですが、ではない時にふくらましでどこまで長さ稼げるか、が 「解がない場合もあるね」になるか否か、ですね

そんな牛刀を持ち出さなくても手計算で解けますね。
のためのstep1として、解がない場合もあるよね、というのを
話を簡単にするために、条件４は後回し、かつ SとGはX軸上にして説明します。
仮に (0,0)-(10,0)とします
これに 条件１ の指定長さが ｌ だとします。SPGでｌになるようなPを置きます。Pの位置はS,Gを焦点とする楕円です。すると角SPGが最大になるのはに二等辺三角形になるときです。ｌが小さければ 条件５を満たしますがｌが大きくなると満たしません。
さて、点を増やせば角度は大きくなるか？
三角形SPGを折りたたんでPが(5,0)になるようにします。角度は変わりません。fanaさんの図を見れば明らか。
X軸を超えて折り曲げても、角度は変わりません。
つまり SGの長さに対して ｌ がある値を越えると解がないです。

step2 では手計算でもできる解
ということで、条件５を満たすPが得られたと！
おめでとう、それが解です
１点ではなぁとか Y軸上の上限があるなら適宜折り畳んでください
条件４はどうなった！  お互いに反対側にPを取れば解決
SGはX軸に並行では無い。それは回転軸移動で計算してください

Answer

前回の質問で，ふわっと

> 条件を満たすことが自明な「複雑でない」経路ペアであればなにかしら用意することは簡単だと思うので，
> そこを出発点にして（常に条件を満たす範囲で）変形させていく的な方向のやり方とかもあるかもしれませんね．
> （最も単純な形状から再分割を繰り返していくみたいな感じ？）

みたいに書きましたが，そんな感じの方針は採れないでしょうか．

---

まず，初期状態として

* 条件2～4 を満たすが
* 「指定された経路長（条件１)」よりも短い

折れ線を用意します．
（下図は話の内容を伝えるために適当に描いただけのものですので，各種条件を満たせてはいないもしれませんが）なんかこんな感じの折れ線からスタートするイメージです．

![イメージ説明](https://ddjkaamml8q8x.cloudfront.net/questions/2025-12-22/12ee6059-ea84-4c97-822d-4312bf3789c1.png)

この状態では上記したように経路長が不足していますので，長くなる方向で経路を変更していきます．

いずれかの経路のいずれかの１辺を選択し→新しく中間点を設けて２つの辺に変化させます．
（言うまでもなく，新しい中間点の位置というのは，経路の変更結果が条件２～４を満たすように，且つ，条件１の経路長を超えないように選びます．）

![イメージ説明](https://ddjkaamml8q8x.cloudfront.net/questions/2025-12-22/62f3bcb0-2b3a-40b6-bc76-602dcacedfe9.png)

これを，２つの経路が条件１を満たすまで繰り返します．

---

## 追記

とりあえず「長さを増やしていくこと」だけを考えると，こんな話↓にはできないのだろうか？
全ての角度を130度としたまま長さを（ある値までなら？？）増やしていけるような気がするけど，どうなんだろう？
![イメージ説明](https://ddjkaamml8q8x.cloudfront.net/questions/2025-12-23/ea54b362-674e-4c13-aedf-e33a2f8991c2.png)

で，最終的に末端部分であれば長さの微調整はできるとかいう話はないかな？
![イメージ説明](https://ddjkaamml8q8x.cloudfront.net/questions/2025-12-23/297d84ca-7196-437e-80f9-a331b63266b8.png)

実現したいこと

発生している問題・分からないこと

該当のソースコード

試したこと・調べたこと

上記の詳細・結果

補足

追記

関連した質問