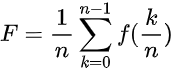まず次のようなグラフを見てみよう。
ここで、次のような問題を考える。
オレンジ色に塗られた部分の面積を求めなさい。
これは、この時点では数学と言うよか小学校の算数だ。
オレンジ色に塗られた部分は三角形なんで、1/2 × 幅 × 高さで50になる、ってのは暗算で簡単に分かる。
JavaScriptでも次のように書けるよな。
node.js
1> 1/2 * 10 * 10
250
3>
オシマイ、だ。
ただ、これは「三角形の面積の公式」であり、対三角形なだけで汎用性はない。大体、あなたが公式を覚えてなければどーしよーもない。ぶっちゃけ、コンピュータよりあなたに負担がかかってる(笑)。
「プログラムを書く」ってのはある関数を書く際にどこまで「汎用性」が追求できるのか、と言うのが一つのテーマになる。これを抽象度を上げる等と表現する。
ただし、ここで、暗算でも計算出来るようなネタにしてるのは、広く知られている「面積を求めるコンピュータ上のアルゴリズム」と言うのが、あくまで近似値にならざるを得ないから、だ。簡単に計算出来るネタの方が、コンピュータが出した解が「どの程度本当の答えに近いのか」見て分かりやすい。
そんなワケで、まずはこう言った簡単なネタにしてる。
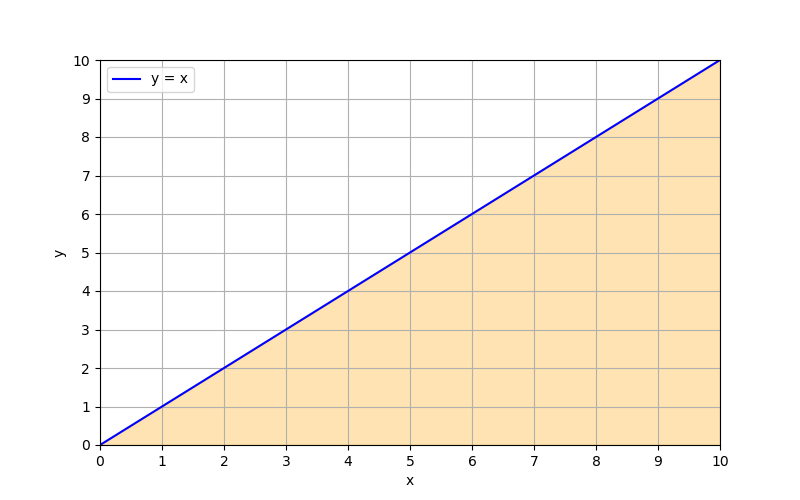
コンピュータで上のグラフが示す範囲の面積を求める場合、良く行われるやり方が、短冊状のブツを敷き詰めて、その総和をもって面積の近似値とする、と言う方法論だ。概念的には次のようなグラフになる。
これは幅が1で高さがy = xよりx、の長方形を9個並べて三角形の面積を近似しようとしている。これを区分求積法と呼ぶ。
ぶっちゃけ、区分求積法はそんなに計算精度は高くない。高くないが、計算精度の高さを今回は問題にしてないし、アルゴリズム自体が簡単なのでこれを使っていく。
上の「長方形を使ってその総和を三角形の面積の近似」をそのままバカ正直にJavaScriptを使って書けば、コードは以下のようになるだろう。
JavaScript
1function calcArea() {
2 return 1 * 0 + 1 * 1 + 1 * 2 + 1 * 3 + 1 * 4 + 1 * 5 + 1 * 6 + 1 * 7 + 1 * 8 + 1 * 9;
3}
あまりにもバカっぽいコードだけど、題意自体は取り敢えず満たせる。積を表す各項は長方形の面積計算(底辺×高さ)を表していて、その総和を取っている。そしてこのcalcAreaの計算結果は45だ。50に5つ程足りないが、「短冊を敷き詰めた」図を見ると分かるが、三角形を埋めきれてない以上当然の結果だ。
あと、関数本体の書き方も良くない。確かに「図が意味してる通り」の計算を詰めてるけど、あまりにもダサいやり方だ。言い換えると面倒くさいコーディングだ。
もう一つ難点が出てくる。区分求積法は、短冊の幅をより小さくしてより数多く敷き詰める事によって精度があがる。
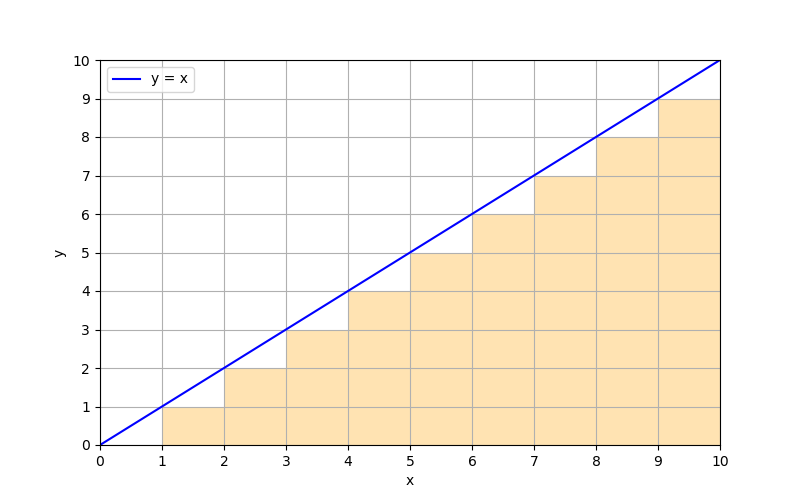
例えば、次のグラフを見てみよう。
今度は短冊(長方形)の幅は1/2、つまり0.5だ。これを対象とする時、一々上のコードを書き換えて、
JavaScript
1function calcArea() {
2 return 1/2 * 0 + 1/2 * 1/2 + 1/2 * 1 + 1/2 * 3/2 + 1/2 * 2 + 1/2 * 5/2 + 1/2 * 3 + 1/2 * 7/2 + 1/2 * 4 + 1/2 * 9/2 + 1/2 * 5 + 1/2 * 11/2 + 1/2 * 6 + 1/2 * 13/2 + 1/2 * 7 + 1/2 * 15/2 + 1/2 * 8 + 1/2 * 17/2 + 1/2 * 9 + 1/2 * 19/2;
3}
みてぇにしたいのか、って話だ(笑)。僕自身も、「解説」目的じゃないとこんなん書かない(笑)。間違いそうで泣きそうになってた(笑)。
いくらグラフを忠実に翻訳してようと、こんなん書きたくないだろう。メンドい。当然だ。
なお、答えは47.5で、前回のクソダサコードよか分割数が多いので、より50へと近づいている。
幅を指定すれば分割数が自動で決まる、ってなればそっちの方がいい筈なんだよな。こういう場合、これは復習になるだろうが、外部から引数を取る、ってカタチにすれば、まず上のような情けないコードを書く必要がなくなる。
そして「幅を指定できる」と言うのはプログラムの抽象度を上げる事を意味するんだ。
いや、さすがに上のようなバカなプログラムを書いたことねぇし。
ってあなたは言うだろう。が、ここで一回、「関数に、何故に引数を取る、と言う機能があるのか」じっくり考えてみて欲しい。
例えば、xの最大値が10、って条件で引数に幅dxを取るとする。既に見たが、dx = 1だと分割数は10になり、dx = 0.5だと分割数は20だ。つまり、分割数 = xの最大値/dxの関係がある。
ここで、JavaScriptでの有名なハックを紹介する。仕様(ECMAScript)上、JavaScriptにはPythonのrange関数(学術的にはiota関数と呼ばれる)が無い。
そこで、次のようなハックが良く用いられている。
node.js
1> [...Array(10/1).keys()]
2[
3 0, 1, 2, 3, 4,
4 5, 6, 7, 8, 9
5]
6> [...Array(10/0.5).keys()]
7[
8 0, 1, 2, 3, 4, 5, 6,
9 7, 8, 9, 10, 11, 12, 13,
10 14, 15, 16, 17, 18, 19
11]
12>
これは確かにハックだ。要はあんま美しくないんだけど、range/iotaに付いての実装法は後述しよう。
注: ECMAScriptにrangeを含めて欲しい、と言う提案はこれまで何度も行われてるんだけど、否決されてきている。JavaScriptは「ブラウザ上で動く」前提のプログラミング言語なんで、Pythonみたいに肥大化させたくない、と言う勢力が強いんだろう。なお、後で見るが、range/iotaも高階関数絡みだ。
さて、上の計算を見ると、配列の長さは丁度分割数になってて、また、要素はindexになっている。これを利用する。
ここでArray.prototype.map()を導入する。こいつは関数じゃないが、コールバック関数を引数に取る高階メソッドだ。
次のようにしてみよう。
node.js
1> [...Array(10/1).keys()].map((x) => x * 1)
2[
3 0, 1, 2, 3, 4,
4 5, 6, 7, 8, 9
5]
6> [...Array(10/0.5).keys()].map((x) => x * 0.5)
7[
8 0, 0.5, 1, 1.5, 2, 2.5, 3,
9 3.5, 4, 4.5, 5, 5.5, 6, 6.5,
10 7, 7.5, 8, 8.5, 9, 9.5
11]
12>
前者は当たり前の結果に見えるが、後者は幅を1/2(0.5)にした時のダサい計算に含まれてる要素である事に気づくんじゃないか。そう、これは各短冊の「開始地点」、つまりx座標である、と解釈可能だ。
現在、対象としてる関数はy=xだ。と言う事はこれらはそのまま「長方形の高さ」だと言う事が出来る。
そして、底辺が「幅」で、前者は幅が1、後者は幅が0.5だ。これらを利用するとコールバック関数を次のように書く事が出来る。
node.js
1> [...Array(10/1).keys()].map((x) => 1 * x * 1)
2[
3 0, 1, 2, 3, 4,
4 5, 6, 7, 8, 9
5]
6> [...Array(10/0.5).keys()].map((x) => 0.5* x * 0.5)
7[
8 0, 0.25, 0.5, 0.75, 1,
9 1.25, 1.5, 1.75, 2, 2.25,
10 2.5, 2.75, 3, 3.25, 3.5,
11 3.75, 4, 4.25, 4.5, 4.75
12]
13>
結果、これら配列要素は上で書いたダサいコードの、計算式の各項になってる。コールバック関数を長方形の面積公式にしたお陰で、あとは総和を取るだけで済む状態になっている。しかし、現行のJavaScript処理系(ECMAScript実装)には「総和を取る関数」が無いので、代わりにArray.prototype.reduceの力を借りよう。
Node.js
1> [...Array(10/1).keys()].map((x) => 1 * x * 1).reduce((x, y) => x + y, 0)
245
3> [...Array(10/0.5).keys()].map((x) => 0.5* x * 0.5).reduce((x, y) => x + y, 0)
447.5
5>
上の計算でArray.prototype.reduceがやってるのは、初期値0に対して与えられた配列の要素を先頭から順番に足していってる。
つまり、
[...Array(10/1).keys()].map((x) => 1 * x * 1) -> 配列を返す -> その配列にreduce((x, y) => x + y, 0) を適用
[...Array(10/0.5).keys()].map((x) => 0.5* x * 0.5) -> 配列を返す -> その配列にreduce((x, y) => x + y, 0)を適用
とメソッドを直接連鎖して書いてるわけだ。
この、返り値が存在するメソッドを連鎖させて計算させるテクニックをそのまんまメソッドチェーンと呼ぶ。
ここまで来れば、短冊の「幅」、dxを引数とする関数calcAreaを書くのは簡単だ。
JavaScript
1function calcArea(dx) {
2 return [...Array(10/dx).keys()].map((x) => dx * x * dx).reduce((x, y) => x + y, 0);
3}
計算結果を見てみよう。
node.js
1> calcArea(1)
245
3> calcArea(1/2)
447.5
5> calcArea(1/10)
649.5
7> calcArea(1/100)
849.9499999999999996
9> calcArea(1/1000)
1049.99500000000002
と、短冊の幅が小さくなればなるほど(つまり、分割数が多くなればなるほど)、計算結果の近似値は、暗算結果、つまり理論値へと近づいて行ってる。
さて、今まではx座標が0から10の範囲で形成する三角形の面積を考えてきた。しかし、x座標が0から20の範囲であるとか、あるいはx座標が0から5の範囲だった場合はどうだろう。今まで書いてきた関数をコピペして、xの最大値が20用の面積計算用関数とか、xの最大値が5用の面積計算関数を別立てすべきなんだろうか。
当然そんな必要はない。引数を増やしてxの最大値を与えるようにすれば解決だ。
JavaScript
1function calcArea(dx, mx) {
2 return [...Array(mx/dx).keys()].map((x) => dx * x * dx).reduce((x, y) => x + y, 0);
3}
繰り返す。関数に引数を取る機能がある最大の理由は、書いてる関数の汎用性を高める為だ。言い換えると関数の抽象度を高める効果がある。また、今書いてる関数で使われてる数値等に具体性を与えない。つまり決定を後回しに出来るんだ。
大事な事なんで2度書こう。実は、プログラミングに於いて、「抽象度が高い」とはほぼ「決定を後回しに出来る」と同義語なんだ。