回答編集履歴
4
タイポ修正
answer
CHANGED
|
@@ -21,7 +21,7 @@
|
|
|
21
21
|
ただし、ここで、暗算でも計算出来るようなネタにしてるのは、広く知られている「面積を求めるコンピュータ上のアルゴリズム」と言うのが、あくまで近似値にならざるを得ないから、だ。簡単に計算出来るネタの方が、コンピュータが出した解が「どの程度本当の答えに近いのか」見て分かりやすい。
|
|
22
22
|
そんなワケで、まずはこう言った簡単なネタにしてる。
|
|
23
23
|
|
|
24
|
-
コンピュータで上のグラフが示す範囲の面積を求める場合、良く行われるやり方が、短冊
|
|
24
|
+
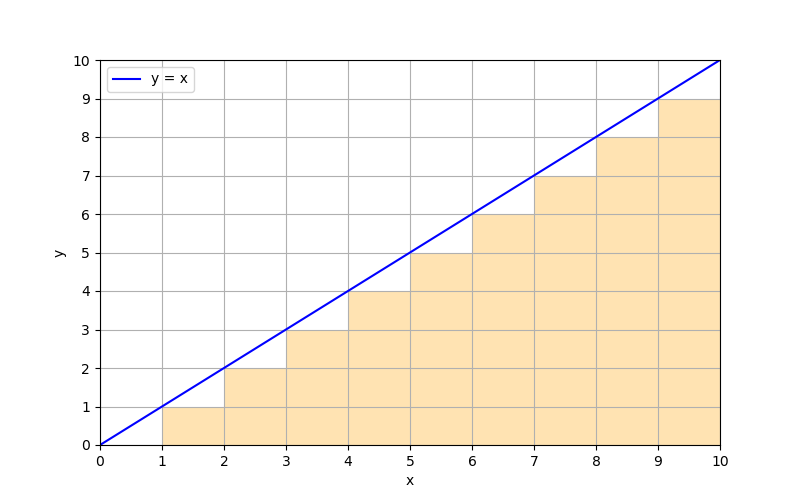
コンピュータで上のグラフが示す範囲の面積を求める場合、良く行われるやり方が、短冊状のブツを敷き詰めて、その総和をもって面積の近似値とする、と言う方法論だ。概念的には次のようなグラフになる。
|
|
25
25
|
|
|
26
26
|
|
|
27
27
|
|
3
助詞を修正
answer
CHANGED
|
@@ -104,7 +104,7 @@
|
|
|
104
104
|
>
|
|
105
105
|
```
|
|
106
106
|
|
|
107
|
-
前者は当たり前の結果に見えるが、後者は幅を1/2(0.5)にした時
|
|
107
|
+
前者は当たり前の結果に見えるが、後者は幅を1/2(0.5)にした時の**ダサい**計算に含まれてる要素である事に気づくんじゃないか。そう、これは各短冊の「開始地点」、つまり`x`座標である、と解釈可能だ。
|
|
108
108
|
現在、対象としてる関数はy=xだ。と言う事はこれらはそのまま「長方形の高さ」だと言う事が出来る。
|
|
109
109
|
そして、底辺が「幅」で、前者は幅が1、後者は幅が0.5だ。これらを利用するとコールバック関数を次のように書く事が出来る。
|
|
110
110
|
|
2
計算式修正
answer
CHANGED
|
@@ -62,7 +62,7 @@
|
|
|
62
62
|
|
|
63
63
|
ってあなたは言うだろう。が、ここで一回、「関数に、何故に引数を取る、と言う**機能**があるのか」じっくり考えてみて欲しい。
|
|
64
64
|
|
|
65
|
-
例えば、``x``の最大値が10、って条件で引数に幅``dx``を取るとする。既に見たが、``dx = 1``だと分割数は10になり、``dx = 0.5``だと分割数は20だ。つまり、分割数 = ``x``/``dx``の関係がある。
|
|
65
|
+
例えば、``x``の最大値が10、って条件で引数に幅``dx``を取るとする。既に見たが、``dx = 1``だと分割数は10になり、``dx = 0.5``だと分割数は20だ。つまり、分割数 = ``xの最大値``/``dx``の関係がある。
|
|
66
66
|
ここで、JavaScriptでの有名なハックを紹介する。仕様(ECMAScript)上、JavaScriptにはPythonの[`range`](https://docs.python.org/ja/3.14/library/functions.html#func-range)関数(学術的には`iota`関数と呼ばれる)が無い。
|
|
67
67
|
そこで、次のようなハックが良く用いられている。
|
|
68
68
|
|
1
形式の再整理
answer
CHANGED
|
@@ -62,7 +62,7 @@
|
|
|
62
62
|
|
|
63
63
|
ってあなたは言うだろう。が、ここで一回、「関数に、何故に引数を取る、と言う**機能**があるのか」じっくり考えてみて欲しい。
|
|
64
64
|
|
|
65
|
-
例えば、``x``の最大値が10、って条件で引数に幅``dx``を取るとする。既に見たが、``dx = 1``だと分割数は10になり、``dx=0.5``だと分割数は20だ。つまり、分割数 = ``x``/``dx``の関係がある。
|
|
65
|
+
例えば、``x``の最大値が10、って条件で引数に幅``dx``を取るとする。既に見たが、``dx = 1``だと分割数は10になり、``dx = 0.5``だと分割数は20だ。つまり、分割数 = ``x``/``dx``の関係がある。
|
|
66
66
|
ここで、JavaScriptでの有名なハックを紹介する。仕様(ECMAScript)上、JavaScriptにはPythonの[`range`](https://docs.python.org/ja/3.14/library/functions.html#func-range)関数(学術的には`iota`関数と呼ばれる)が無い。
|
|
67
67
|
そこで、次のようなハックが良く用いられている。
|
|
68
68
|
|
