">>"で1/4になるのは分かるのですが、kが奇数のとき、k^2 / 4は小数となるはずなのに、
python3において >>などのビット演算は、整数を引数にとり、演算結果も整数です。
Python3 - 6.8. シフト演算 (shifting operation)
ビット演算ですので、2進数表記のビット単位で考えないと動きが分かりづらいと思います。2ビットシフトすると1/4になるのは結果的にそうなる場合があるというだけで、実際は右シフトするごとに最下位ビットは消えます。ですので奇数の場合でも 3 --> 1.5 --> 0.75 などとなるわけではありません。
下に、整数 7 を1ビットずつ右シフトする例を示してみます。
bash
1$ python3
2Python 3.6.8 (default, Feb 15 2019, 01:54:23)
3[GCC 7.4.0] on cygwin
4Type "help", "copyright", "credits" or "license" for more information.
5>>> k = 7
6>>> print(k, bin(k))
77 0b111
8>>> print(k >> 0, bin(k >> 0))
97 0b111
10>>> print(k >> 1, bin(k >> 1))
113 0b11
12>>> print(k >> 2, bin(k >> 2))
131 0b1
14>>> print(k >> 3, bin(k >> 3))
150 0b0
16>>> print(k >> 4, bin(k >> 4))
170 0b0
18>>>
追記しました:2019/04/21 10:18
k ** 2 >> 2でk以下の奇数の数 * 偶数の数を求められる訳が依然として分かりません。
もしよろしければ、そちらについても解説していただけないでしょうか?
とコメントをいただいたので解法の意味するところまで考えていましたが、投稿直前に解決してしまいましたね。KSwordOfHasteさんの回答は私にとっても参考になったのですが、せっかく書いたので、考察のひとつとして追記しておきます。(間違いなどあればご指摘大歓迎です)
k ** 2 >> 2 は、解法として (k // 2) * ((k + 1) // 2) とほぼ同じ意味合いを持っていると思います。冗長部分を削ぎ落としたショートカット(近道)と言って良いでしょうか。
k = 11として、python3での(k // 2) * ((k + 1) // 2)式を一般の数式に当てはめてみます。(整数での演算なので、小数点以下は切り捨てられますが)
(11 ÷ 2) × ((11 + 1) ÷ 2) = 5 × 6 = 30
これは、11 × (11 + 1) ÷ 2 ÷ 2 と変形できます。縮めれば 11 × 12 ÷ 4 です。答えは33になってしまいますが、考え方は同じように見えます。変形したために(11 ÷ 2)がなくなるので、小数部分が欠落せず、計算が合いませんがこれは仕方ありません。対して、k ** 2 >> 2 を一般の数式に当てはめて見てみると 11 × 11 ÷ 4 = 30 です。前述の式とほぼ同じです。
。。。納得行きませんか? そうですね。私もなんか釈然としませんでした。発想を変えて、k ** 2 >> 2 の式の意味するところを考えてみます。
ひとまず偶数奇数を考えず、kを二乗するのは、全組み合わせ数を求めるためのものとします。数が大きくなると面倒なので、k = 7とします。
まず、単純に全部の組み合わせ数を求めると、7 × 7 = 49 です。

問題の求めるところは奇数と偶数のペアですから、偶奇が同じぺアは除外します。ここで1/2 します。
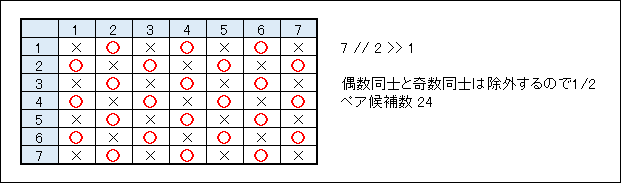
各組み合わせにおいては(1, 2)と(2, 1)は同じですから、それらは除外します。つまり、ここで更に1/2します。

1/2 を2回するわけで、1/4 、つまり 右2ビットシフト >> です。k ** 2 >> 2 は この工程、(全組み合わせ数) ÷ 4 を表現したプログラミングと見ることができると思います。
AtCoderの該当の回答者さんがどういう思考でこの式に辿りついたか私には伺い知れませんが、なるほど、と思いました。実は私もこのAtCoder A問題を過去に解いたことがあったのでコードを見直してみたのですが、晒すには恥ずかしいほどに愚直な方法で解いていました。
以上、ご参考までとなります。







退会済みユーザー
2019/04/20 18:05
退会済みユーザー
2019/04/21 02:02