Pythonで行列の計算をしたい。

Question

Pythonで行列の計算をし，パラメータを算出したいです．xとyの値は例として挙げています．予定ではクリックで点を生成し，その点をふやしていくことを考えています．つまり点の個数が決まっていなくても，図のような行列の計算はできますでしょうか．最終的な結果としてcというパラメータの値を取り出したいです．
よろしくお願い致します．

(追記)
手計算によって求めた解を載せます。また，これらの行列は離散点を3次スプライン補間をする際の3次多項式のパラメータの一部(ｃ)を求める式になります。
よろしくお願い致します。

x	y
0	0
1	3
4	3
5	1
8	2

Comments

[can110]

まずは点の数がたとえば５個と決まっている場合はコードは書けますでしょうか？
書けない場合でも、A,bおよびcを手計算で求めた結果を提示ください。
さらに、この問題、数式に名前（～の式、～の解法など）がある場合はそれを提示ください。

[can110]

Aの最も右下の値は0ではなく1のはずではないでしょうか？
またb=[ 0 -9 -6 7 0]ではないでしょうか？
今一度、数式または手計算の結果が正しいか確認ください。

[takes.it.easy]

どちらもおっしゃる通りです。再度計算すると
b=[0, -9, -6, 7, 0]
c=[0, -0.930556, -0.518519, 0.939815, 0]
となりました。

Answer 1

x,yにリストとして座標を追加し、numpyの配列に変換すれば以下のソースコードで計算できると思います。
Ax=rとして解いた。a,b,c,dは三次関数の係数。

import numpy as np

x = np.array([0, 1, 4, 5, 8])
y = np.array([0, 3, 3, 1, 2])
n = len(x)-1
h = x[1:]-x[:-1]
a = y

# 対角成分
Adiag = np.eye(n+1)
Adiag[1:-1, 1:-1] *= 2*(h[:-1]+h[1:])

# 対角成分の一つ下の斜めの成分
Alower = np.eye(n+1, k=-1)
Alower[1:, :-1] *= h
Alower[-1, -2] = 0

# 対角成分の一つ上の斜めの成分
Aupper = np.eye(n+1, k=1)
Aupper[:-1, 1:] *= h
Aupper[0, 1] = 0

A = Adiag + Alower + Aupper

# Aの逆行列
Ainv = np.linalg.inv(A)

r = np.zeros(n+1)
r[1:-1] = (3/h)[1:]*(a[2:]-a[1:-1])-(3/h)[:-1]*(a[1:-1]-a[:-2])

c = np.dot(Ainv, r)

d = (c[1:]-c[:-1])/(3*h)
b = (a[1:]-a[:-1])/h-h/3*(2*c[:-1]+c[1:])
print("x", x, "y", y)
print("h", h, "a", a)
print("A")
print(A)
print("r", r)

print("a", a)
print("b", b)
print("c", c)
print("d", d)

x [0 1 4 5 8] y [0 3 3 1 2]
h [1 3 1 3] a [0 3 3 1 2]
A
[[1. 0. 0. 0. 0.]
 [1. 8. 3. 0. 0.]
 [0. 3. 8. 1. 0.]
 [0. 0. 1. 8. 3.]
 [0. 0. 0. 0. 1.]]
r [ 0. -9. -6.  7.  0.]
a [0 3 3 1 2]
b [ 3.31018519  2.37962963 -1.96759259 -1.5462963 ]
c [ 0.         -0.93055556 -0.51851852  0.93981481  0.        ]
d [-0.31018519  0.04578189  0.48611111 -0.10442387]

Comments

[takes.it.easy]

丁寧な回答をありがとうございます。
お聞きしたいのですが、
　h = x[:1] - x[:1]
という記述は，
　h = x[i] - x[i-1]
と同様に扱ってもよいものなのでしょうか。

[Penpen7]

h = x[1:]-x[:-1]は
for i in range(1, len(x)):
h = x[i]-x[i-1]
と同等になりますね。
x[1:]は要素x[1]からx[n-1]までの配列を表しており、
x[:-1]は要素x[0]からx[n-2]までの配列を表しています。
これを上から下に引くと, x[1]-x[0], x[2]-x[1], ... , x[n-1]-x[n-2]
の成分をもつhが得られ, for文を使わなくとも一括で複数のデータが得られることになります。
かなりこのソースコードではnumpyのスライス機能を使っているので、初めはわかりにくいのかもしれませんが、慣れるとfor文を書かずに済み、実行速度が上がり、ソースコードがスッキリします。
もちろんfor文で貪欲に書いてもいいですが、その分反復回数が増えると遅くなります。

[takes.it.easy]

ありがとうございます。
スプライン曲線を描く際，このコードではノンパラメトリックとして計算されていると思いますが，xは短調増加でなくてはならない制限を解決したく、パラメトリックの式として描画したいと考えています。パラメトリックな3次多項式とするにはどのようにすればよういでしょうか。変数をtとおいたときのx,yの式やパラメータの算出などご教授いただけると幸いです。

[Penpen7]

パラメトリックの式ではxは任意の順序でもスプライン曲線を描けるという理由が申し訳ありませんが、わかりませんでした...
それよりもxが常に単調増加するように座標を挿入するところを選んで挿入するか、スプライン曲線を描く前にxとyの対応を崩さないようにxをソートしてから各パラメータを求めるようにするのが自然なように感じます。例えば, xとyの対応を崩さないようにソートする場合は
y = y[np.argsort(x)]
x = np.sort(x)
でxを単調増加数列に変えることができます。
なお、スプライン曲線は三次関数を滑らかに繋いでいるにすぎないため、三次関数をパラメータ表示できるかということと同値ですが、それは可能だと思います。（が、やって効果はあるかは不明です)

[Penpen7]

媒介変数表示しても一切やることは変わらないので(文字が入れ替わるだけ)、回答を参考に改変してください。

Answer 2

パラメータ表示でやってみた。

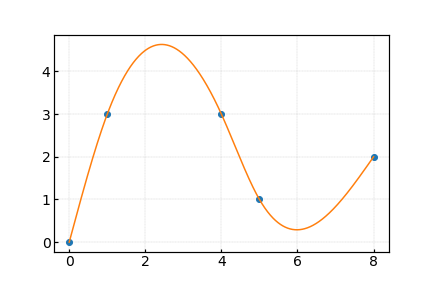
import numpy as np
import matplotlib.pyplot as plt

# スプライン曲線のパラメータを求める。
def calculateSplineParameter(x):
    # t = 0,1,2,...,x.size-1とする。
    n = x.size-1
    h = np.ones(n)
    a = x

    # 対角成分
    Adiag = np.eye(n+1)
    Adiag[1:-1, 1:-1] *= 2*(h[:-1]+h[1:])

    # 対角成分の一つ下の斜めの成分
    Alower = np.eye(n+1, k=-1)
    Alower[1:, :-1] *= h
    Alower[-1, -2] = 0

    # 対角成分の一つ上の斜めの成分
    Aupper = np.eye(n+1, k=1)
    Aupper[:-1, 1:] *= h
    Aupper[0, 1] = 0

    A = Adiag + Alower + Aupper

    # Aの逆行列
    Ainv = np.linalg.inv(A)

    r = np.zeros(n+1)
    r[1:-1] = (3/h)[1:]*(a[2:]-a[1:-1])-(3/h)[:-1]*(a[1:-1]-a[:-2])

    c = np.dot(Ainv, r)
    d = (c[1:]-c[:-1])/(3*h)
    b = (a[1:]-a[:-1])/h-h/3*(2*c[:-1]+c[1:])

    return [a,b,c,d]

# 三次関数の係数から, 元の点から間の点を求める。
def calculateInterpolationPoints(splineParameter, orignalPointsNumber, interpolationPointsNumber=1000):
    a, b, c, d = splineParameter
    
    index = np.repeat(np.arange(orignalPointsNumber-1), interpolationPointsNumber, axis=0)
    t = np.tile(np.linspace(0, 1, interpolationPointsNumber), orignalPointsNumber-1)
    
    return a[index] + b[index]*t + c[index]*t**2 + d[index]*t**3

# 補間したい点の座標
x = np.random.rand(20)
y = np.random.rand(x.size)

parameterX = calculateSplineParameter(x)
parameterY = calculateSplineParameter(y)

X = calculateInterpolationPoints(parameterX, x.size)
Y = calculateInterpolationPoints(parameterY, y.size)

plt.plot(X, Y, label="spline curve")
plt.plot(x, y, marker='o', linestyle='None', label='original points')
plt.legend()
plt.savefig("graph.png", dpi=200,figsize=(4,3))

周期3次スプライン曲線を使って閉曲線にしました。
Periodic cubic smoothing splines as a quadratic
minimization problem

import numpy as np
import matplotlib.pyplot as plt


# 周期3次スプライン曲線のパラメータを求める。
def calculatePeriodicSplineParameter(x):
    # t = 0,1,2,...,x.size-1とする。
    n = x.size - 1
    h = np.ones(n)
    a = x

    # 対角成分
    Adiag = np.zeros((n, n))
    Adiag[1:, 1:] = np.diag(2 * (h[:-1] + h[1:]))
    Adiag[0][0] = 2 * (h[-1] + h[0])
    Alower = np.diag(h[:-1], k=-1)
    Aupper = np.diag(h[:-1], k=1)

    A = Adiag + Alower + Aupper
    A[-1][0] = h[-1]
    A[0][-1] = h[-1]

    # 対角成分
    Vdiag = np.zeros((n, n))
    Vdiag[1:, 1:] = np.diag(-(1 / h[:-1] + 1 / h[1:]))
    Vdiag[0][0] = -(1 / h[-1] + 1 / h[0])
    Vlower = np.diag(1 / h[:-1], k=-1)
    Vupper = np.diag(1 / h[:-1], k=1)

    V = Vdiag + Vlower + Vupper
    V[-1][0] = h[-1]
    V[0][-1] = h[-1]

    r = 3 * np.dot(V, a[:-1])

    c = np.linalg.solve(A, r)

    c = np.insert(c, c.size, c[0])

    d = (c[1:] - c[:-1]) / (3 * h)
    b = (a[1:] - a[:-1]) / h - h / 3 * (2 * c[:-1] + c[1:])
    a = a[:-1]
    c = c[:-1]
    return [a, b, c, d]


# 三次関数の係数から, 元の点から間の点を求める。
def calculateInterpolationPoints(splineParameter,
                                 interpolationPointsNumber=1000):
    a, b, c, d = splineParameter
    assert (a.size == b.size == c.size == d.size)
    index = np.repeat(np.arange(a.size), interpolationPointsNumber, axis=0)
    t = np.tile(np.linspace(0, 1, interpolationPointsNumber), a.size)
    return a[index] + b[index] * t + c[index] * t**2 + d[index] * t**3


# 補間したい点の座標
x = np.random.rand(100)
y = np.random.rand(x.size)
x = np.insert(x, x.size, x[0])
y = np.insert(y, y.size, y[0])

parameterX = calculatePeriodicSplineParameter(x)
parameterY = calculatePeriodicSplineParameter(y)

X = calculateInterpolationPoints(parameterX)
Y = calculateInterpolationPoints(parameterY)

plt.plot(X, Y, label="spline curve")
plt.plot(x, y, marker='o', linestyle='None', label='original points')
plt.legend()
plt.savefig("graph.png", dpi=200, figsize=(4, 3))

Comments

[takes.it.easy]

ありがとうございます。
勉強させていただきます。

Answer 3

予定ではクリックで点を生成し，その点をふやしていくことを考えています．

上記を実現するため、クラスを使って以前の状態を保持しておく例です。
なお、点の追加において、x値`は単純増加で与える（制御点が左側にぐるっと戻らない）ことが前提です。

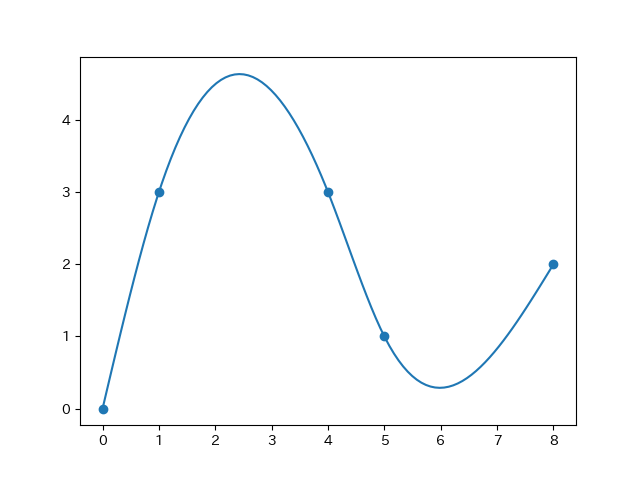
import numpy as np
import matplotlib.pyplot as plt

# ３次スプライン補間法
# http://www.civil.kumamoto-u.ac.jp/matsu/spline.pdf

class Spline:
    # xys : 最低３点ある配列
    def __init__(self, xys):
        self.xys = np.array(xys)
        N = self.xys.shape[0]
        assert N >= 3

        self.h = np.array([self.xys[i,0]-self.xys[i-1,0] for i in range(1,N)])
        self.a = self.xys[:,1]

        self.A = np.eye(N)
        for i in range(2,N):
            self.A[i-1,i-2:i+1] = self.get_A_line(i)

        self.r = np.zeros(N)
        for i in range(2,N):
            self.r[i-1] = self.get_r_val(i)

    # 指定行のAの値を計算して返す
    def get_A_line(self, i):
        return [self.h[i-2], 2*(self.h[i-2]+self.h[i-1]), self.h[i-1]]

    # 指定位置のrの値を計算して返す
    def get_r_val(self, i):
        return 3*(self.a[i]-self.a[i-1])/self.h[i-1] - 3*(self.a[i-1]-self.a[i-2])/self.h[i-2]

    # 新たな点を追加
    def add(self,xy):
        self.xys = np.vstack([self.xys, np.array(xy)])
        N = self.xys.shape[0]
        self.h = np.append(self.h, self.xys[N-1,0]-self.xys[N-2,0])
        self.a = self.xys[:,1]

        Anew = np.zeros((N,N))
        Anew[0:N-1,0:N-1] = self.A
        self.A = Anew
        self.A[N-2,N-3:N] = self.get_A_line(N-1)
        self.A[N-1,N-1] = 1

        self.r = np.append(self.r, 0)
        self.r[N-2] = self.get_r_val(N-1)

    # パラメータを算出
    def calc_param(self):
        Ainv = np.linalg.inv(self.A)
        self.c = np.dot(Ainv, self.r)
        N = self.xys.shape[0]
        self.b = np.array([ (self.a[i]-self.a[i-1])/self.h[i-1] - self.h[i-1]/3*(2*self.c[i-1]+self.c[i]) for i in range(1,N)])
        self.d = np.array([ (self.c[i]-self.c[i-1])/(3*self.h[i-1]) for i in range(1,N)])

    # 補間されたy値を返す
    def get_y(self, x):
        xs = self.xys[:,0]
        if x < xs[0] or x > xs[-1]:
            return 0
        elif x == self.xys[0,1]:
            return xs[0]
        elif x == xs[-1]:
            return self.xys[-1,1]

        # 区間を決定
        i = 0
        while True:
            if xs[i] > x:
                break
            i += 1
        i -= 1

        dx = (x-xs[i])
        return self.a[i] + self.b[i]*dx + self.c[i]*dx*dx + self.d[i]*dx*dx*dx


sp = Spline([[0,0],[1,3],[4,3]]) # 初期の３点は最初に与える
sp.add([5,1])
sp.add([8,2])
sp.calc_param()

print(sp.r)# [ 0. -9. -6.  7.  0.]
print(sp.a)# [0 3 3 1 2]
print(sp.b)# [ 3.31018519  2.37962963 -1.96759259 -1.5462963 ]
print(sp.c)# [ 0.         -0.93055556 -0.51851852  0.93981481  0.        ]
print(sp.d)# [-0.31018519  0.04578189  0.48611111 -0.10442387]

# 描画
xs = np.linspace( np.min(sp.xys[:,0]), np.max(sp.xys[:,0]), 100)
ys = np.array([sp.get_y(x) for x in xs])
plt.scatter(sp.xys[:,0], sp.xys[:,1])
plt.plot(xs, ys)
plt.show()

Comments

[takes.it.easy]

丁寧な回答ありがとうございます。
こちらのコードではxは単純増加ということですが、自由な曲線を描くために、媒介変数t(0≦t≦1)を用いて、補間したいと考えています。媒介変数でスプライン補間をする場合、それぞれのパラメータはどのように決めるのでしょうか。

[can110]

> こちらのコードではxは単純増加ということですが
もともとの数式、考えが単純増加を前提としていると思うのですが、違いますでしょうか？

> 自由な曲線を描くために～
そのようにできる数式、考えはどのようなものでしょうか？

[takes.it.easy]

もともとの式はxが決まるとyが決まってしまうため、コースを一周するような曲線を描くことができません。そこで変数tを用いて媒介変数表示してみたらどうかと考えています。
t = [0,1]
h = t_i+1 - t_i

x(t) = a_x + b_x * t + c_x * t^2 + d_x * t^3
a_x,i = x_i
y(t) = a_y + b_y * t + c_y * t^2 + d_y * t^3
a_y,i = y_i

よろしくお願いします。
参考サイト：https://tajimarobotics.com/cubic-spline-interpolation-parameter/

[can110]

なるほど。
まずは固定の点の数で動くコードを書いてみてはいかがでしょうか？

Answer 4

できるかとという問いでしたら、できます。
numpy.insert()とかで行と列を拡張していけばいいんではないでしょうか。