オライリー社「pythonではじめる機械学習」94～95ページ、3次元空間で線形SVMで見つかった決定境界をもとの２つの特徴量として表示するコードで理解できない部分があります。

Question

プログラミングと機械学習の初心者です。Windous10、anaconda3、JupyterNotebookを使用しています。
オライリー社「pythonではじめる機械学習」2.3.7.1線形モデルと非線形特徴量の94～95ページのコードで大きく2点ほど理解できない部分があります。
コードは、sklearnのmake_blobsデータセットを用いて、拡張された3次元空間で線形SVMで見つかった決定境界を、もとの２つの特徴量の関数として表示するものになります。

• 以下14行目のコードでXX、YY、ZZをそれぞれ(50,50)から(2500,)に変換しているようなのですが、これはdecision_functionがこの形式しか受け付けないからでしょうか。また、decision_functionは何をしているのでしょうか。fitと同じように決定境界を学習しているのでしょうか。

dec=linear_svm_3d.decision_function(np.c_[XX.ravel(),YY.ravel(),ZZ.ravel()])の部分

• 以下15行目のコードでXX,YYの右にdec.reshape(XX.shape)が入るのはなぜでしょうか。これは(2500,)のdecを(50,50)にしているようですが、なぜXX,YY,ZZではないのでしょうか。確かにここをZZに置き換えると決定境界線が平行線に作図されてしまってうまくいかないのは確認できたのですが、なぜなのか理解できません。

plt.contourf(XX,YY,dec.reshape(XX.shape),levels=[dec.min(),0,dec.max()],cmap=mglearn.cm2,alpha=0.5)

以上よろしくお願いいたします。
以下、コード全体となります。

import mglearn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
X,y=make_blobs(centers=4,random_state=8)
y=y%2
X_new=np.hstack([X,X[:,1:]**2])
from sklearn.svm import LinearSVC
linear_svm_3d=LinearSVC().fit(X_new,y)
xx=np.linspace(X_new[:,0].min()-2,X_new[:,0].max()+2,50)
yy=np.linspace(X_new[:,1].min()-2,X_new[:,1].max()+2,50)
XX,YY=np.meshgrid(xx,yy)
ZZ=YY**2
dec=linear_svm_3d.decision_function(np.c_[XX.ravel(),YY.ravel(),ZZ.ravel()])
plt.contourf(XX,YY,dec.reshape(XX.shape),levels=[dec.min(),0,dec.max()],cmap=mglearn.cm2,alpha=0.5)
mglearn.discrete_scatter(X[:,0],X[:,1],y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

Answer 1

以下14行目のコードでXX、YY、ZZをそれぞれ(50,50)から(2500,)に変換しているようなのですが、これはdecision_functionがこの形式しか受け付けないからでしょうか。

np.c_[XX.ravel(),YY.ravel(),ZZ.ravel()] ですが、

1. XX, YY, ZZ はそれぞれ (50, 50) の2次元配列であり、ndarray.ravel() でそれぞれ (2500,) の1次元配列に変更しています。
2. numpy.c_[XX.ravel(),YY.ravel(),ZZ.ravel()] で3つの1次元配列を横方向に結合しているので、(2500, 3) の2次元配列になります。

この (2500, 3) の2次元配列を decision_function() に渡しています。

また、decision_functionは何をしているのでしょうか。fitと同じように決定境界を学習しているのでしょうか。

学習自体は fit() で完了しています。
decision_function() は、点を与えると、SVM が学習した分離超平面からの距離を返します。

sklearn.svm.LinearSVC.decision_function

以下15行目のコードでXX,YYの右にdec.reshape(XX.shape)が入るのはなぜでしょうか。これは(2500,)のdecを(50,50)にしているようですが、なぜXX,YY,ZZではないのでしょうか。

dec.reshape(XX.shape) としているのは、contourf() の仕様上、dec の形状 (2500,) を XX, YY に合わせて (50, 50) にしなければいけないためです。

コードの流れ解説

線形分離できない2次元のデータが与えられたとします。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC

# 2次元のデータを作成する。
X, y = make_blobs(centers=4, random_state=8)
y = y % 2

fig, ax = plt.subplots()
class_colors = ListedColormap(["g", "k"])
ax.scatter(X[:, 0], X[:, 1], c=y, cmap=class_colors)
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
plt.show()

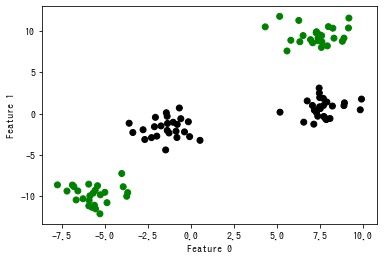
このままでは線形分離できないので、Φ: (x, y) → (x, y, y^2) という関数で3次元空間に射影します。3次元空間上に射影したことで線形分離可能になったので、線形 SVM で学習できます。

X_new = np.hstack([X, X[:, 1:] ** 2])

fig = plt.figure(figsize=(7, 7))
ax = fig.add_subplot(111, projection="3d")
ax.scatter(X_new[:, 0], X_new[:, 1], X_new[:, 2], c=y, cmap=class_colors)
ax.view_init(30, 30)
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
plt.show()

fit() で学習します。

svc = LinearSVC().fit(X_new, y)

射影した空間 {(x, y, y^2)|x, y∈ℝ} 上の各点と分類超平面との距離を decision_function() で計算します。

# 射影した空間上の点を作成する。
xs = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
ys = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)
XX, YY = np.meshgrid(xs, ys)
ZZ = YY ** 2

# 作成した点と分類超平面との距離を計算する。
dist = svc.decision_function(np.c_[XX.ravel(), YY.ravel(), ZZ.ravel()])

# SVM の超平面を計算する。
def hyper_plane(svc, XX, YY):
    a1, a2, a3 = svc.coef_[0]
    b = svc.intercept_[0]
    return (-b - a1 * XX - a2 * YY) / a3


plane = hyper_plane(svc, XX, YY)


# 可視化する。
fig = plt.figure(figsize=(9, 7))
ax = fig.add_subplot(111, projection="3d")
# 学習データの点を可視化する。
ax.scatter(X_new[:, 0], X_new[:, 1], X_new[:, 2], c=y, cmap=class_colors)
# 射影した空間上の各点と分類超平面との距離を可視化する。
sc = ax.scatter(XX, YY, ZZ, c=dist, cmap="bwr", vmin=-15, vmax=15)
# 分類超平面を可視化する。
ax.plot_surface(XX, YY, plane, alpha=0.5)
ax.view_init(30, 30)
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
fig.colorbar(sc)
plt.show()

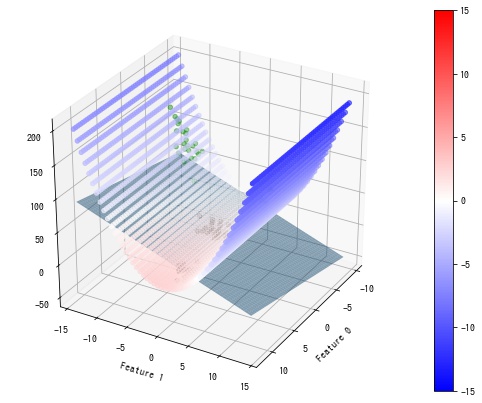
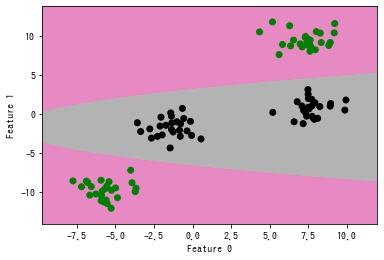
{(x, y)|decision_function(x, y, y^2) = 0, x, y∈ℝ} が元の2次元空間において、決定境界となります。
なので、decision_function(x, y, y^2) = 0 である等高線を contourf() で描画します。

fig, ax = plt.subplots()
class_colors = ListedColormap(["g", "k"])
# 決定境界を可視化する。
ax.contourf(
    XX, YY, dist.reshape(XX.shape), levels=[dist.min(), 0, dist.max()], cmap="Set2"
)
# データを可視化する。
ax.scatter(X[:, 0], X[:, 1], c=y, cmap=class_colors)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()

Comments

[meg_]

質問の例題は「線形モデルと非線形特徴量」の項目のものです。2次元では分離不可なデータの分類を学習するものとなっています。

[tiitoi]

話の流れがいろいろ間違っていたので修正しました。
コメントありがとうございます。

[searabbit]

大変丁寧な解説をいただきありがとうございます。直感的にもとてもわかりやすかったです。
いただきましたコードの細かい内容についてはこれからじっくり咀嚼していきたいと思いますが、なんとか話についていけている感じです。
一点だけ確認させてください。いただきましたコード中のdist（質問のコードではdecに相当する部分）は、結局は各点と分類超平面のz軸方向の距離という理解でいいでしょうか。

[tiitoi]

```
xs = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
ys = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)
XX, YY = np.meshgrid(xs, ys)
ZZ = YY ** 2
```
これで作ったのが、回答3個目の図のU上の点です。
この各点と分類超平面 (薄い青の平面) との符号付きの距離が dist です。
3つめの図だと分類超平面から上側に離れていくほど負の値 (青色)、下側に離れていくほど正の値 (赤色) になっています。

> 各点と分類超平面のz軸方向の距離という理解でいいでしょうか。

「点と平面との距離」は「点から平面に下ろした垂線の距離」と定義されます。

[searabbit]

なるほど！よくわかりました！
ありがとうございました！

Answer 2

decision_functionはf=wx+bの計算で識別面からのマージンを計算してます。
(50,50)から(2500,)に変換は、f=wx+bの形ですのでxはベクトルにする必要があります。

余計なお世話かもしれませんが、今の理解で本を先にススメるは難しいかもしれませんよ。
単回帰→重回帰→ロジスティック回帰の分類→ＳＶＭの分類の順で理解を深めることをオススメします。

Comments

[searabbit]

ご指摘いただきました件、確かにSVMの頁に入った途端、突然難易度が上がった感じです。もう少し基礎固めに時間を割くべきなのかとも感じています。もし、比較的初心者向けでおススメできる書籍などがありましたら、ご紹介いただけますと幸いです。よろしくお願いいたします。

[s-uchi]

私は、本を買っては挫折してを繰り返した人間（このループにハマる人結構いると思います。）ですが
今思うと、本は最初に手にしたアマゾン等の評価がいいもんでいいと思います。

足りてないのは、知識ではなく”経験”だと思います。
なので、オススメは参考書の各トピック毎に、xxx 実践とかでググって興味をソソられる記事を見つけてコード書いてみるといいです。
例えば、「ＳＶＭ、実践」でググッて、その実践コードを模写するのではなく、チラ見しながら書く or 解こうしている問題だけ把握して、あとは参考書ベースにコード書いてみる等の手を動かすことがオススメです。

[searabbit]

貴重な経験談とアドバイスありがとうございます。
確かにキーワード検索してみると色々出てきますね。
自分のレベルにあったものを見つけて試行錯誤してみたいと思います。
ありがとうございました。