2分法で等高線を求めたものの、期待通りの答えにならない。

Question

###前提・実現したいこと
物理学が専門の大学院生です

二変数関数f(x,y)=cを満たす(x,y)をたくさん求めるプログラムをC言語を用いて、二分法で考えました。しかし、f(x,y)の等高線を数式処理ソフトで書かせた場合と一部一致しません。

###発生している問題・エラーメッセージ

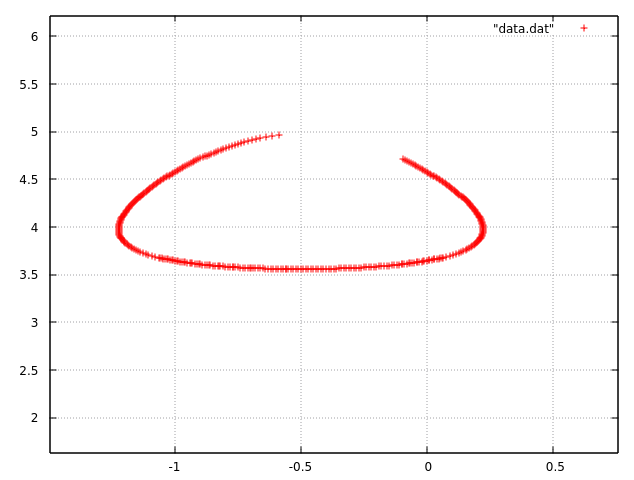
左の赤いラインが二分法によって求めたf(x,y)=1.54をみたす点(x,y)をプロットしたもの。一方で、右の青い図が数式処理ソフトによって出力された関数f(x,y)の等高線。二分法でもとめた点(x,y)の一部がかけているのはなぜでしょうか。

###該当のソースコード

include <stdio.h>
include <math.h>
double f(double,double);

void main(void){
  double x,xmin,xmax,xmid,y,eps;
  int cnt,cntlimit,i,m;
  FILE *file;
  
  eps=0.001;
  cntlimit=100000;

  file = fopen("data.dat","w");
  cnt=0;
  
  for(i=-500;i<=500;i++){

    y=2.0+i/100.0;
    xmax=2.5;
    xmin=0.0;
    
  do{
    cnt ++;
    xmid=(xmax+xmin)/2.0;
    
    if( f(xmin,y)*f(xmid,y)<0.0) xmax=xmid ;
    else xmin=xmid;
   
  }while( fabs(xmax-xmin)>eps && cnt < cntlimit );

   if(cnt==10000) fprintf(file,"It doesnt converge \n");
   else if( fabs(f(xmid,y))>0.01 ) fprintf(file,"0\t0\n");
   else fprintf(file,"%f\t%f\n",xmid,y);
   

  }

  for(i=-500;i<=500;i++){

    y=2.0+i/100.0;
    xmax=-0.0;
    xmin=-2.5;
    
  do{
    cnt ++;
    xmid=(xmax+xmin)/2.0;
    
    if( f(xmin,y)*f(xmid,y)<0.0) xmax=xmid ;
    else xmin=xmid;
   
  }while( fabs(xmax-xmin)>eps && cnt < cntlimit );

   if(cnt==10000) fprintf(file,"It doesnt converge \n");
   else if( fabs(f(xmid,y))>0.01 ) fprintf(file,"0\t0\n");
   else fprintf(file,"%f\t%f\n",xmid,y);
   

  }
  
  
  fclose(file);
}

double f(double kx,double ky){
  double c=1.98;
  double w2p,w2d,eE,t,s,d,Ec,Ev;

  t=-1;
  s=0;
  d=1;
  eE=0.5;
  
  w2p=3+4*cos(sqrt(3)*(kx+eE)/2.0)*cos(ky/2.0)+2*cos(ky);
  w2d=3+4*cos(sqrt(3)*(kx-eE)/2.0)*cos(ky/2.0)+2*cos(ky);

  Ec=(2*t*s*w2p+sqrt(d*d-d*d*s*s*w2p+4*t*t*w2p))/(2-2*s*s*w2p);
  Ev=(2*t*s*w2d-sqrt(d*d-d*d*s*s*w2d+4*t*t*w2d))/(2-2*s*s*w2d);
  
  return Ec-Ev-c ;
  
}

###関数f(x,y)の具体的な形
参考までに関数f(x,y)の具体的な形を載せておきます。

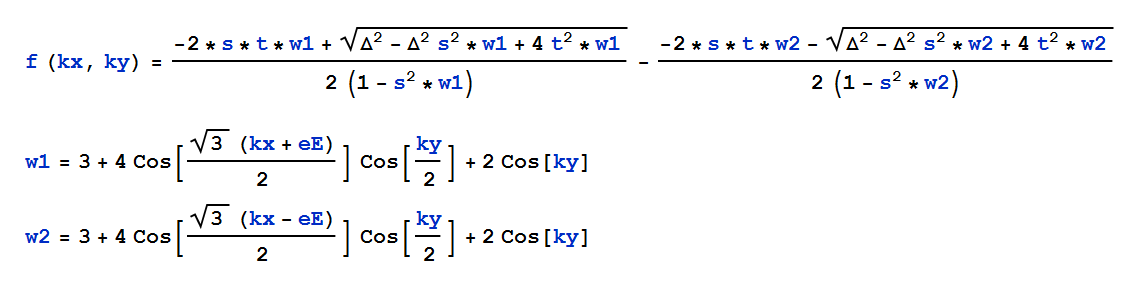
ここで、t=-1,s=0,d=1,eE=0.5として上のグラフは求めましたが、より一般にこれらの値を変化させて等高線の図の変化を考察するのが目的でした。

###補足情報
二分法以外のアルゴリズムでの解法がある場合はこちらのご投稿いただけますと幸甚に存じます。

Answer 1

Evの途中からw2dがw2pになってるのは合ってますか？

二分法の判定のところ・・・f(xmin,y)*f(xmid,y)<0.0 なんですけど、
ここではyは定数として考えることが出来ると思うんです。

つまり、判定は f(x)がxに対して単調であれば、計算による誤差がないという理想的な状況下で
二分法によって正しく求まるとは思いますが、0<=x<=2.5や-2.5<=x<=0の範囲で、
f'(x) は必ずしも正で固定か、負で固定だと言い切れますか？

微分して求めるとこれはわかると思います。確認してもし言い切れないなら、
今回の最適化で二分法を用いること自体が間違っていると思います。

物理学専攻なら、自分で複雑な関数を定義し、最適化の計算方法も細かくプログラムできるようになることはハードルが高すぎると思います。科学技術計算で最近よく使われるPythonを使えるようになるというのはどうでしょうか？信頼性が高く、内部でC言語を呼び出すため、計算もそこそこ速いモジュールがたくさん公開されています。機械学習や大量のデータの整形など、便利なモジュールもあり、これからの科学技術計算のユーザーが使う言語としての将来性はダントツだと思います。

C言語で正しい数値計算を追及しだすと、本業に使うべき時間が奪われることになりそう...
信頼性のある計算方法で出した評価でなければ何の意味もないだろうし...

Comments

[physics303]

ご丁寧にありがとうございます。
Evの式に関して、僕が間違えていました。これを修正したところ、期待していた等高線の図がかけました。

yが固定されたとき、f'(x)がxによって正になったり負になったりすると、二分法では求まらないということでしょうか。つまり、二分法で求められるのはfが単調増加or単調減少の場合のみということであっていますか？

自分の所属している研究室ではPtyhonよりもFortranが主流です。Ptyhonでは、上のような計算は比較手容易に可能なモジュールがあるということでしょうか？

細部まで見ていただきありがとうございます。

[退会済みユーザー]

とりあえず解決したみたいでよかったです。

言葉が足りなかったかもしれません。すいません。
解を探す範囲として-2.5<=x<=0, 0<=x<=2.5というふうにそれぞれ設定されていますが、二分法で解が少なくともひとつ求まるためには、関数が解を探す範囲[α,β]で連続であって、f(α)*f(β) <=0 あれば十分です。つまり、解を探す範囲として、[α,β]を正しく設定することはとても重要です。ここで、関数が単調であれば、αを限りなく小さい数、βを限りなく大きい数にとることで、解がある場合には正しく求まります。
つまり、言いたかったことは、-2.5<=x<=0　の範囲で解を探すことをどうやって決定したのか、もしある決定方法をとったのなら、それをほかの可変なパラメータを動かしたときにも対応できるような初期条件の決定方法として一般化することができるのか、ということです。今回の場合、解がひとつ求まればなんでもいいというわけではなさそうです。yが固定でも解として２つ以上のXが対応しうるので...
となると、正しい初期条件の決定方法を、吟味しながら決めるしかなさそうです。

私はMATLABについてよく知らなかったのですが、今見てみたら、MATLABはかなり数値計算で余計なことを考えなくでもいいように整備されていると感じました。Pythonを新しく学ぶぐらいなら、すでに使えるMATLABでもいいのかも...
ただ、速度を気にするならMATLABにしてもやり方を学ぶ必要はありそうです。
しかし、C言語やFortranとなると途端にハードルが高い感じがします。
誤差を小さくするために式変形をして、計算順序を考えて、といちいちやるのは厳しすぎますよ

[退会済みユーザー]

間違えました。physics303さんが使えるのはMathematicaですね笑
Mathematicaでもいいんじゃないですか？

[physics303]

ありがとうございます。よく分かりました。

MathematicaではFindInstanceという関数をつかってf(x,y)=cをみたす(x,y)を求めることができますが、これはfが複雑になると計算時間が長くなってしまいます。今回、計算するfでは一つ(x,y)をみつけるのに数分かかってしまいます。そのため、CやFortranで数値計算ができないものかなと相談しました。

もしかしたらMathematicaでもう少し早い方法があるのかもしれませんが、見つけることができませんでした。（私のまわりでMathematicaを使っている人がいなくて・・・）