SmoothFollow.csの分からない箇所に関して。

Question

前提・実現したいこと

Unity標準アセットのSmoothFollow.csのコードについて、
処理が分からない箇所があるのでご教示お願いします。

該当のソースコード

メインカメラにアタッチしました。

	public class SmoothFollow : MonoBehaviour
	{

		// The target we are following
		[SerializeField]
		private Transform target;
		// The distance in the x-z plane to the target
		[SerializeField]
		private float distance = 10.0f;
		// the height we want the camera to be above the target
		[SerializeField]
		private float height = 5.0f;

		[SerializeField]
		private float rotationDamping;

		[SerializeField]
		private float heightDamping;

		// Use this for initialization
		void Start() { 
		}

		// Update is called once per frame
		void LateUpdate()
		{			
			// Early out if we don't have a target
			if (!target)
				return;
 
			// Calculate the current rotation angles
			var wantedRotationAngle = target.eulerAngles.y;
			var wantedHeight = target.position.y + height;

			var currentRotationAngle = transform.eulerAngles.y;
			var currentHeight = transform.position.y;

			// Damp the rotation around the y-axis
			currentRotationAngle = Mathf.LerpAngle(currentRotationAngle, wantedRotationAngle, rotationDamping * Time.deltaTime);

			// Damp the height
			currentHeight = Mathf.Lerp(currentHeight, wantedHeight, heightDamping * Time.deltaTime);

			// Convert the angle into a rotation
			var currentRotation = Quaternion.Euler(0, currentRotationAngle, 0);

			// Set the position of the camera on the x-z plane to:
			// distance meters behind the target
			transform.position = target.position;
			transform.position -= currentRotation * Vector3.forward * distance;

			// Set the height of the camera
			transform.position = new Vector3(transform.position.x ,currentHeight , transform.position.z);

			// Always look at the target
			transform.LookAt(target);
			

		}
	}

試したこと

ソースコードを上から読んでいき、下記コード辺りまではおそらく理解できました。

var currentRotation = Quaternion.Euler(0, currentRotationAngle, 0);

currentRotationは、Y軸周りの角度に関して、
thisのY軸の角度から、targetのY軸の角度に変化していくものかと思います。
また、Heightに関する処理のコードも理解できていると思います。

質問

・質問1。
理解しているつもりですが、念のため質問です。
currentRotationのコードについて、
transform.eulerAngles.yをtarget.eulerAngles.yに変えていると思いますが、
これは、thisのZ軸の向きを、targetのZ軸の向きに合わせているという認識で合っていますか？

・質問2。
こちらのコードがわかりません。

  transform.position = target.position;
  transform.position -= currentRotation * Vector3.forward * distance;

　まず、1行目は、thisをtargetの位置に持ってきているかと思いますが、
ここから、2行目で、「currentRotation * Vector3.forward * distance」の分だけ
移動させているかと思うのですが、
Vector3.forward * distanceに、左からcurrentRotation * を掛けているのが、
どのようなベクトルになるかがわかりません。
仮にコードが下記であれば、イメージは付きます。

  transform.position = target.position;
  transform.position -= Vector3.forward * distance;

　追記。
クォータニオンとベクトルの掛け算について考えました。
・質問2-1。
this.transform.rotationにベクトルdirを掛けたものは、

　this.transform.rotation * dir

　「thisのローカル軸を基準に伸びるベクトルdir」という認識で合っていますか？
そう考えると、
・質問2-2。
「『Rotation(クォータニオン) * dir(ベクトル)』は、『Rotationの回転軸を基準に伸びるベクトルdir』」
という認識で合っていますか？

・質問3。
質問2の時点のコードが理解できていないので、さらにその先もわからないのですが、

　transform.LookAt(target);

　これのコードをコメントアウトするのとしないのとでは、カメラの動きが大きく変わる理由がわかりません。
「transform.LookAt(target);」これ自体のコードは、
thisのZ方向の向きをtargetに向かせるだけの処理かと思うのですが、
これをコメントアウトするのとしないのとでは、なぜこんなにも処理が大きく変わってしまうのでしょうか？

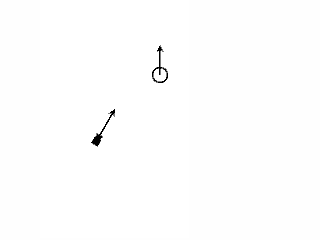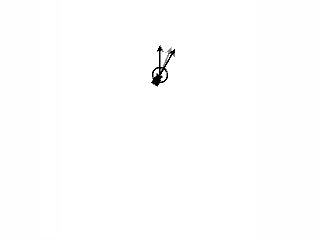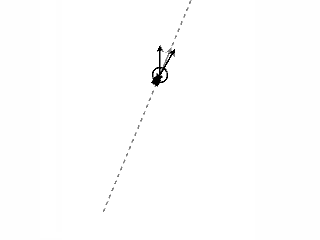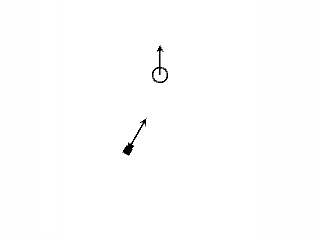
・ゲーム実行前。
targetは球です。
球のZ軸の向きはワールドのZ軸の向きと同じです。


・LookAtをコメントアウトしてゲームを実行した場合。
その場で、targetの方向に向きました。
currentRotationでは、thisのZ軸の向きを、targetのZ軸の向きに合わせていたかと思うのですが、
thisのZ軸の向きがtargetのZ軸の向きと合っていないというのも、
質問2に関係することかと思いますが、わかりません。

・LookAtを有効にした場合。
図のオレンジ色の矢印の軌跡をゆっくり描いて最終的に図のようになりました。
今度はthisのZ軸の向きがtargetのZ軸の向きに合っているようです。
ただ、thisのZ方向の向きをtargetに向かせるだけの「transform.LookAt(target);」の処理を
有効にしただけのはずなのに、なぜ急にオレンジ色の矢印の軌跡移動をするようになったのかわかりません。

Answer 1

質問1について
そうですね、真上から見たときの自身の向きを次第にターゲットの向いている方向へ向けていく動きになるでしょう。

質問2について
質問2-1はおおむねそんな感じのとらえ方でいいように思います（以前「ローカル座標とワールド座標のベクトルの変換」で申し上げたような珍妙な座標系を使っていない限りは...）。
質問2-2も質問2-1からの類推ということでおっしゃりたいことは何となくイメージできますが、ちょっともやっとした表現ではありますね（「回転軸を基準に」といいましても回転軸は3本ではなく1本ですし、その1本も回転後の基底ベクトル3本のどれかと必ずしも一致するわけではないですし...）。もっと単純に「あるベクトルをあるクォータニオンで回した結果」とか、あるいはベクトルを位置ベクトルと見なして「ある座標系上の点を、その座標系の原点を中心に、その座標系上での回転を表現するクォータニオンを使って回転移動した移動先の位置」とかではどうでしょうか。
currentRotation * Vector3.forwardは要するに「向きを自身の前方向からターゲットの前方向に少しだけ近づけた方向」を指していますので、それに沿ってdistanceの分だけカメラを後退させることになるでしょう。

質問3について
LookAtなしの場合ですが、おそらく画面に映るターゲットの水平位置はごくわずかに画面の水平中心からずれているんじゃないでしょうか?

LookAtによって、このズレの分だけカメラの向きがごくわずかに回転するはずです。これによりカメラの向きが徐々に目標方向に近づいていくでしょう。また、カメラの向きが少しずつ回ることによって次回のtransform.position -= currentRotation * Vector3.forward * distance;でカメラが移動する位置もずれるはずです。

一方、LookAtがないとカメラの向きはいつまで経っても元の向きのままになります。結果としてcurrentRotationも変化せず、transform.position -= currentRotation * Vector3.forward * distance;でカメラが移動する位置も毎回同じになってしまう...ということになりそうです。

Comments

[退会済みユーザー]

ご回答ありがとうございます。
質問1についてよく考えたのですが、
「this.transform.eulerAngles.yをtarget.eulerAngles.yに合わせるということは、
　thisのZ軸の向きを、targetのZ軸の向きに合わせているということ」
に関してですが、汎用的に考えたときの暗黙の前提条件に気づいていなかったのですが、
これはもちろん、「this.transform.up == target.transform.upならば、」
(「thisのY軸の向きがtargetのY軸の向きと同じならば、」)
という前提条件が必要という認識で合っていますか？
ただ、smoothFollowのようなプレイヤー(target)を追従するカメラにアタッチするようなコードならば
プレイヤーが斜めによろけて、target.transform.upがワールドのY軸とずれても、
カメラ(this)のほうは、this.transform.upをtarget.transform.upに合わせずに、
今回のコードのように、
this.transform.rotaion = Quaternion.Euler(0, target.eulerAngles.y, 0);
になるように、thisのY軸(this.transform.up)は、ワールドのY軸に合わせておいたほうが、
追従カメラとして適切、と思いました。

質問2について。
質問2-1のご意見ありがとうございます。
質問2-2のご指摘ありがとうございます。
クォータニオンが所々理解できていなかったので、間違った表現、解釈となってしまっていました。
なるほど、ベクトルをクォータニオンで回したものと考えられるのですね。
transform.position -= currentRotation * Vector3.forward * distance;
のイメージがわかりました。ありがとうございます。

質問3について。
すみません、自分の理解力が乏しくて、少々考えるお時間をいただけたらと思います。
解説の図までご提示いただけているのに申し訳ないです。
transform.LookAtをコメントアウトしたときの挙動からまだ理解できていない状態でして。
transform.LookAtをコメントアウトしても、
currentRotationAngle = Mathf.LerpAngle(currentRotationAngle, wantedRotationAngle, rotationDamping * Time.deltaTime);
は効いているはずなので、
currentRotationAngleであるtransform.eulerAngles.y、つまり、this(カメラ)のZ方向は、
wantedRotationAngleであるtarget.eulerAngles.y、つまり、targetのZ方向に向こうとする動きを続けるはずなのに、なぜ向かないのであろうという疑問からハマってしまっていまして。

[Bongo]

おっしゃるように、本当にぴったり3次元的にtransform.forwardの向きを合わせるには「this.transform.up == target.transform.upならば」という条件を入れるべきかと思いますが、真上から見たときのtransform.forwardの向きであればtransform.upがずれていてもtransform.eulerAngles.yを合わせるだけで十分のように思います。シーン上で適当なオブジェクトをぐるぐる回し、Y角度を操作してみるといいのではないでしょうか。

「currentRotationAngle = Mathf.LerpAngle(currentRotationAngle, wantedRotationAngle, rotationDamping * Time.deltaTime);」があるのにtargetのZ方向に向いていかない...ということについては、たしかにcurrentRotationAngleはこの行を通過すると少しだけwantedRotationAngleに近づきはするのですが、LookAtがない場合は、結局その近づいた後のcurrentRotationAngleがカメラの位置の移動だけに使われて、回転には反映されていないためと言えるでしょう。
LateUpdateが終わってもtransform.eulerAngles.yに変化がなく、次回LateUpdateに入ったときにもその変化のないtransform.eulerAngles.yが再びcurrentRotationAngleに代入されて元に戻ってしまうわけですね。

[退会済みユーザー]

ご回答ありがとうございます。
ご教示いただいたおかげと数時間考えた甲斐もあって、徐々に理解できてきました。

なるほど、真上から見たときでは問題ないですね。

色々考えた結果、また質問が増えてしまいました、申し訳ないです。

質問1。
transform.LookAt(target)をコメントアウトして、カメラのY軸の回転が変化していないのを確認しました。
transform.position -= currentRotation * Vector3.forward * distance;
を理解していたつもりでしたが、「Rotation」の文字が入っていて、
なんとなく回転もかかっているような錯覚をしていました。
ベクトルをクォータニオンで回しても、ベクトルのままでしたね。
transform.positionに入れられるものもベクトル(Vector3)なので、
transform.positionに値を入れる(Vector3を入れる)ということは、
transformの位置を設定しているだけであって、transform自身には回転はかからないということですか？

質問2。
あと、横道に逸れてしまって申し訳ないのですが、
クォータニオンとベクトルの演算に関して調べていたとき、
「Unityは左手系座標」というワードや「掛ける順番が大事」と言ったワードを見つけたりして、
下記を明言しているサイトは見つからなかったのですが、

「あるベクトルをあるクォータニオンで回した結果のベクトルは、
　左手系座標のゲームエンジンの場合は、
　クォータニオン * ベクトル
　で表現でき、
　右手系座標のゲームエンジンの場合は、
　ベクトル * クォータニオン
　で表現できる」
という認識で合っていますか？
(全くの予想なので見当外れなことを言っているかもしれません。)
(試してみた所、Unity(左手系座標)では「ベクトル * クォータニオン」とするとエラーになるみたいですね。)

質問3。
あとすみません、
transform.position = target.position;
transform.position -= currentRotation * Vector3.forward * distance;
このコードを見た時に、違和感があったのですが、
今頃、重大な勘違いをしていることに気づいたかもしれないのですが、
上記1行目の「transform.position = target.position;」は描画されないですか？
つまり、Start関数やUpdate関数などで、
位置・回転・拡大縮小などの変更処理を行っても、
それぞれ個々に最後に行った処理の変更が描画されて、途中の処理は描画されないということで合っていますか？
(位置ならば最後に上書きした位置が描画され、回転ならば最後に上書きした回転が描画される、というようにです。)
実際に下記のコードを試してみたのですが、描画されているようには見えなくて、
コメントの通りで合っていますか？

void Update(){
target.transform.position = new Vector3(9, 3, 5); //この位置に来ているけど描画はされない。
target.transform.position = new Vector3(11, 3, 5); //この位置に来ているけど描画はされない。
target.transform.position = new Vector3(10, 3, 5); //この位置で描画される。
}

質問4。
回転の方の動きを理解する為に、currentHeightに関する行はコメントアウトしていて、
そしてさらにLookAtの行をコメントアウトしたら、回転(currentRotationAngle)は変化するはずがないのに、
カメラがガクガク震える挙動は何なんだろうと悩んでいたのですが、
これはもしかしたら、Time.deltaTimeが毎フレーム違う値を取るから、
Mathf.LerpAngleの結果が変わってくるということでしょうか？
しかも、ここでさらに気づいたのですが、シーン上で何かしらの選択ツールでカメラを選択しないと
振動が再現されませんでした。
選択ツールでカメラを選択するのとしないのとでは、シーン上のみならず、
ゲーム画面でも、振動するしないの差異が出てくるので、ちょっとわからなくなってきましたが、
やはり、根本はTime.deltaTimeの影響でしょうか？
→すみません、コメントアウトして試せばいいことに気づき、試してみたところ、
　振動が消えました。
また、余談ですが、Time.deltaTimeを使えば、振動表現できるのかなと思って検索してみたのですが、
意外と記事は見つかりませんでした。

質問5。
currentHeightなんですが、イージング処理のはずなので、
収束しないのでは？と気になって、LookAtの前の行でログを取ってみたのですが、
しばらくしたら、固定値のログを吐き続けたのですが、
これはToString("G")では出力されないレベルで値が変化しているということですか？
Debug.Log(transform.position.y.ToString("G"));
transform.LookAt(target);

肝心のカメラの遅延追従の動きですが、
こちらはご教示いただいたおかげで、
LookAtにより、transform.eulerAngles.yが変わって、
currentRotationAngleが変化し、動きが変わっていくことが理解できました。
ありがとうございます。

[Bongo]

質問1についてはその通りですね。positionを変化させると、オブジェクトの姿勢は維持されたまま平行に移動するはずです。

質問2については、これは特にそのようなルールはないでしょう。左右両手でフレミングのポーズをしてみたとき、左手系では左手の、右手系では右手の親指をX軸、人差し指をY軸、中指をZ軸に見立てることができます。これらは互いに鏡写しの対称になっており、どちらの世界でも座標や姿勢の計算式の形は同じで、計算式を見ただけでは右手なのか左手なのか区別することはできないはずです。
おそらく、「ベクトルと行列の積を表現するとき、ベクトルを行ベクトルととらえて『右に行列、左にベクトル』とする流派と、ベクトルを列ベクトルととらえて『左に行列、右にベクトル』とする流派がある」といった話と混同されてはいませんでしょうか?
こういった環境による違いとして「右手系か左手系か」、「列ベクトルか行ベクトルか」、「配列データを行列と解釈するとき、要素を列優先で詰めるか行優先で詰めるか」などがあってややこしいですね。行列とベクトルの左右は「列ベクトルか行ベクトルか」と関係していて、「右手系か左手系か」とは関係ない話かと思います。「列優先（Column-major），行優先（Row-major）は複数ある - Qiita」（https://qiita.com/suzuryo3893/items/9e543cdf8bc64dc7002a ）や「右手系とか左手系とか回転とかの話 - ぬうぱんの備忘録」（http://nu-pan.hatenablog.com/entry/2016/07/12/225637 ）などの記事がご参考になるでしょうか（なお記事中に「ちなみに、これ以外の組み合わせは聞いたこと無いので辞めたほうがいいと思います」とありますが、Unityはこれ以外に該当する「左手系かつ列ベクトル」ですね...）。
それともう一つ、「行列とベクトルの積」ではなく「クォータニオンとベクトルの積」というのはUnity特有の表現方法でして、実際には「ベクトルをクォータニオン型に変えて、回転クォータニオンを左からかけ、回転クォータニオンの共役クォータニオンを右からかけ、得られた結果のクォータニオンからXYZ成分を取り出してベクトル型に戻す」といったややこしい手順をとることになります（参考：https://qiita.com/kenjihiranabe/items/945232fbde58fab45681#quaternion-%E3%81%A8%E5%9B%9E%E8%BB%A2%E5%A4%89%E6%8F%9B%E3%82%88%E3%81%86%E3%82%84%E3%81%8F%E3%83%8F%E3%82%A4%E3%83%A9%E3%82%A4%E3%83%88 ）。「クォータニオンとベクトルの積」はこの手順を*演算子1つで簡単に書けるようにしたものというわけです。また、ベクトルをクォータニオンで回す場合は上記の「列ベクトルか行ベクトルか」といった差異の影響を受けず、式の形は同じになります。
ややこしい話をいくつも矢継ぎ早にお出しして申し訳ないです...お時間のあるときにじっくりご調査いただくのがいいかと思います。

質問3についてはお気付きの通りですね。一般的にはレンダリングが行われるのは各フレームごとに1回です。1フレーム内でpositionやら何やらが変更されるたびにいちいちレンダリングし直しても無駄でしょうしね...
https://docs.unity3d.com/ja/current/Manual/ExecutionOrder.html の図の中に「OnApplicationPause」から出て「FixedUpdate」に入るループ矢印がありますが、これが一つのフレームに相当します。このループ内の「Scene rendering」と表示されたグレーの枠の部分で実際にシーン上のオブジェクトが描画されることになるでしょう。

質問4について、ご推察の通りそれはdeltaTimeの影響と言えるでしょう。オブジェクトの姿勢が変化しない場合は、計算式の中で変化する因子はdeltaTimeだけですしね。
カメラを選択するかどうかで振動が変化する件については、Unityの内部処理がどうなっているか詳しく調べたわけではないですが、想像するにカメラ選択状態だと計算処理量が増え（シーンビュー上にカメラの視界を表す枠を描いたり、インスペクターの表示を更新したり...）、deltaTimeが変動しやすくなって振動が目に見えるほど大きくなったためじゃないかと思います。
この現象を振動効果として利用しようというのは柔軟な発想で面白いと思いましたが、実際のゲームに使うのはちょっとまずいんじゃないですかね...?
deltaTimeは実行環境や処理負荷に応じてUnityが勝手に調整する値であり、プログラマーが自由にコントロールできるものではないため、たとえ意図したものであってもゲームのプレイヤーにとっては「処理が重くなるとガタガタする粗悪なゲームだ」と思われてしまうかもしれません。

質問5については、確かに数学的には目標値へ無限に近づいていき値はわずかずつ変化し続けるはずですが、プログラム内部の値としては本当に一定値になって、それ以降ずっと変わらなくなっているものと思われます。
有限の精度のfloat型で無限の精度の実数を表現するのは無理な話でして、1回の変化量が小さくなりすぎて有効桁数の限界を超えてしまえば処理前後で値が変わらなくなるでしょう。
ちなみに、有限の時間内では一定値に落ち着かないことを指して「収束しない」とおっしゃっているのだろうとは推察できるのですが、今回のイージング処理のように無限の果ての極限で特定の値に至るのであれば、数学的には「収束する」と言っていいんじゃないかと思います。揚げ足取り的ですみません...

[退会済みユーザー]

ご回答ありがとうございます。

質問1について。
ご回答ありがとうございます。理解できました。

質問2について。
おっしゃる通り、ベクトルと行列の積の表現などいろいろと混同していました。
ご提示のリンクを拝見しました。
クォータニオンと行列に関するお話はまだ理解できないので、
後々勉強していきたいと思います。
「クォータニオンとベクトルの積」はUnity特有の表現方法だったのですね。
「ベクトルをクォータニオン型に変えて、～(中略)～を取り出してベクトル型に戻す」の
ご説明ありがとうございます。
実際に行われている処理の概要がわかって勉強になりました。
Unreal Engineにも少し手を出しているので、Unity特有の表現ということもわかってよかったです。
(もしかしたら、Unreal Engineでも独自の方法で似たような処理ができることもあるかもしれませんが、
そのときは調べます。)

質問3について。
各フレームごとに1回の描画だったのですね。
下記のコードも試してみて、Updateの方の位置では描画されず、LateUpdateの方の位置のみで
描画されることも視認いたしました。

void Update(){
target.transform.position = new Vector3(5, 3, 5); //LateUpdateで変更している為、描画はされない。
}

void LateUpdate()
{
target.transform.position = new Vector3(10, 3, 5); //この位置で描画される。
}

質問4について。
なるほど、そういったことが原因でdeltaTimeが変動しやすくなった可能性が考えられるわけですね。
そうでしたね、deltaTimeは実行環境などによって差異があるものでしたね。
deltaTimeを理解できていたつもりでしたが、まだ考えが浅かったです。ご指摘ありがとうございます。
カメラを揺らすスクリプトですが、検索してみたら、Random.Rangeを使っていたり、
また過去に購入したエフェクトアセットにおまけでカメラを揺らすスクリプトがあったのを思い出したので、そういったものを勉強して実装したいと思います。

質問5について。
とんてもないです、正しい数学用語を教えていただきありがとうございます。
間違った言葉を使っていたので勉強になります。
学生時代に数学で極限を扱った際の収束の概念を微かに思い出しました。検索して確認致しました。

すみません、また長くなってしまって申し訳ないですが、最後の質問をさせていただけたらと思います。

念の為確認させていただきたいのですが、
イージングのLerp処理ですが、第3引数の補間値が1以上にならない限り、
数学的には終了値へ無限に近づいていき値はわずかずつ変化し続けるものの、
プログラム内部の値としては(実際のUnityでは)、float型の有効桁数の限界を超えてしまえば、
最終的に「固定値に留まる」(値は変化しなくなる)という認識で合っていますか？
(そう仰っていると思いますが、くどくてすみません、一応確認させていただきたくなりました。)

気になっているのは、前回のLerp処理の質問で、
イージングのLerp処理は、第3引数の補間値が1以上にならない限り、
永遠に終了値に到達しないと教わり(＝これを値変化が永遠に続くと勘違いしていました)、
終了値に合わせる方法として、Approximatelyメソッドを教わったので、
いかなるときもイージングのLerp処理では、Approximatelyメソッドを終点合わせに使おうと決めていたのですが、固定値に留まるのであれば、必ずしもそうする必要はないと思ったことです。
今回のようなカメラワークは、厳密に終了値に合わせる必要はないと思いますし、
Unity公式のコードとは言え、ずっと動き続けていて気持ち悪いなと勘違いしていたのですが、
これも終点合わせをしなくても停止するということで合っていますか？
あとは厳密に終了値に来させる必要がある場合や、イージングの終わりを検知する必要がある場合は、
やはり、Approximatelyメソッドなどによる終点合わせ処理は必要になるのかなとも思いました。
例えば、コルーチンの毎フレーム繰り返し処理でイージングのLerp処理を実装した場合などは、
終点合わせを行って、イージングの終了を検知させることによって、
動かしているコルーチンを停止させる必要があるのかなと思いました。
ご助言のほどお願いできればと思います。

[Bongo]

そうですね、状況によってはわざわざループ内に条件判定を入れて目標値ぴったりになるようにしてやる必要はないと思います。
今回のカメラの場合にしても、おそらくカメラは目標地点・目標角度にごくわずかだけ足りない地点で動かなくなるんじゃないかと思いますが、その「ごくわずか」というのは位置計算や回転計算で日常的に発生する誤差の幅と同程度かそれよりも小さい幅のはずですので、いちいち目標値合わせをすることを考慮しなくてもいいでしょう。
数学的に考えると動き続けるというのが気持ち悪く感じるのもわからなくもないですが、もし仮に精度が無限で、先に申し上げたような精度的な問題で値が変化しなくなる現象がなかったとしても、その動きは極めてわずかで人間の目には止まっているのと同じに見えるでしょうね。

イージングの終了点を検知する必要がある場合の件についても適切な考えだと思います。イージングの動きの後に次の処理を行いたい場合には終了点を知る必要があるでしょう。
他にも、最終的に目標値にぴったり到達しないと困る場合には終了点を検知して目標値合わせを行う必要があるはずです。
たとえば値を0.0から100.0までイージングさせて、ゲーム上の表示では小数点以下を切り捨てて整数として表示するつもりだった場合、下記のようにシミュレーションしてみると...

using UnityEngine;
public class LerpValue : MonoBehaviour
{
private void Start()
{
var currentValue = 0.0f;
var integerValue = 0;
var previousValue = 0.0f;
var targetValue = 100.0f;
do
{
previousValue = currentValue;
currentValue = Mathf.Lerp(currentValue, targetValue, 0.1f);
integerValue = Mathf.FloorToInt(currentValue);
Debug.Log($"{integerValue} ({previousValue:G9} -> {currentValue:G9})");
} while (currentValue != previousValue);
Debug.Log($"Terminal value:{integerValue}");
}
}

コンソールの最後の5回の出力は下記のようになり...

99 (99.9999466 -> 99.9999542)
99 (99.9999542 -> 99.9999619)
99 (99.9999619 -> 99.9999695)
99 (99.9999695 -> 99.9999695)
Terminal value:99

99.9999695まで到達するとLerp後も値は99.9999695で変化せず、それを小数点以下を切り捨てて整数化した画面上の最終的な表示も99までにしかなりませんでした。最終的に100の表示が出て欲しいなら目標値合わせが必要でしょう（この例だとFloorToIntの代わりにRoundToIntで丸めるのでもよさそうですが）。

参考情報としてですが、ケースによっては別のイージング方式の方が有利かもしれません。「目標時間で目標値に到達する」ということが重要な場合では、今回の方式ではイージング終了タイミングをコントロールしにくく不利のような気がします。
こういう場合に便利なイージングとして、Robert Pennerさんによる各種計算式をよく見かけるように思います（一覧表：https://easings.net/ ）。Lerpと組み合わせる場合は開始値と終了値は固定しておいて（Lerp後の値を次の開始値にするのではなく）、開始時刻から終了時刻にかけて0.0から1.0へ線形に変化する値を用意してやり、さらにその0.0～1.0の値を各種イージング関数を通して変調させ、その値をLerpの第3引数に渡してやればさまざまな緩急を表現できるかと思います。

[退会済みユーザー]

ご回答ありがとうございます。

数学的には値が永続的に変化する処理でも、
プログラムではその値を扱っている型の有効桁数を超えてしまえば、
値が固定されるということがわかり、勉強になりました。

なるほど、仮に精度が無限であったとしても影響はなさそうということですね。

コードのご提示ありがとうございます。拝見しました。
やはりそういった目的のコードだと終了値に合わる必要がありますよね。

イージングのご提示ありがとうございます。
なるほど、Lerpの第3引数の0.0～1.0の変化自体を
イージング関数を通して変調させることで、
目標時間で目標値に到達し、なおかつそれがイージングで表現できるということですね。
とても勉強になります。
こちらも後に勉強したいと思います。

詳細なご解説、たくさんのご教示ありがとうございました。
分からなかったことが全て理解できました。
本当にありがとうございました。

[退会済みユーザー]

ベストアンサーを付けさせていただいた後に、また質問で申し訳ないのですが、
いろいろ弄ってたら気になってしまったのと、自分の理解が正しいか確認させていただきたくなりまして、すみません。
お時間のあるときにご回答いただけたら幸いです。

今回のコードに限っては、下記のように
LerpAngleの戻り値を別の変数に代入しても同じ処理となりますか？

float currentRotationAngle2 = Mathf.LerpAngle(currentRotationAngle, wantedRotationAngle, rotationDamping * Time.deltaTime);
Debug.Log(currentRotationAngle2);

(省略)

// Convert the angle into a rotation
var currentRotation = Quaternion.Euler(0, currentRotationAngle2, 0);

つまり、
「currentRotationAngle = Mathf.LerpAngle(currentRotationAngle, wantedRotationAngle, rotationDamping * Time.deltaTime);
は、この戻り値のcurrentRotationAngleをtransform.rotaionに反映させるのならば、
回転に影響を与えるので(次回のcurrentRotationAngleに反映されるので)、
イージング処理となるけれども、今回は、transform.positionで位置の反映として使っているので、
次回のcurrentRotationAngleに反映されないので、
上記Mathf.LerpAngleはイージング処理になっていない。
これより、今回は新しい変数currentRotationAngle2に書き換えたものでも、同じ結果の処理になる
(回転に影響を与えているのはLookAtだけ)」
という認識で合っていますか？
コードの形としてはイージング処理っぽいけど、今回のMathf.LerpAngleだけの処理に限っては違うのかなと気になってしまいました。

ただ、それでも(currentRotationAngle2に書き換えても)イージング処理っぽい動きに見えるのは、
transform.position -= currentRotation * Vector3.forward * distance;
の繰り返し処理の位置更新によって、だんだんLookAt(target)で向く角度がtargetに近づいて行って、これにより、transform.eulerAngles.yも、target.eulerAngles.yに近づいていくので、コード全体の結果として回転もイージング処理になっているということでしょうか？

何度もすみません。

[Bongo]

はい、今回の場合はLerpAngleの結果を受け取るのを別の変数に変えても問題ないはずです。
後半部分の解釈も妥当だと思います。たとえば「transform.position = Vector3.Lerp(transform.position, targetTransform.position, damping * Time.deltaTime);」のようなシンプルなものでしたら、その一行だけでtransform.positionのイージング処理を表していると言えるでしょうが、今回のケースでは「新しい向きを求める」「新しい向きに基づいてカメラの位置を変更する」「新しい位置に基づいてカメラの回転を変更する（新しい位置からターゲットを注視する）」のステップが複合されることによって、全体としてカメラの位置・回転のイージング処理になっているということですね。

[退会済みユーザー]

ご回答ありがとうございます。
なるほど、ご提示いただいたようなシンプルなコードだとイージング処理ですね。
理解がより一層深まりました。
大変ありがとうございます。