python3にて指定されたパターンを使って、目標の順序までの並び替えにかかる最小回数の算出方法

Question

1年ほど前から、独学でPython3をちょこちょこ進めている初学者です。
腕試しがてら、「０～４まで書かれたカードを特定のパターンらでの入れ替えを繰り返し、目標の順番になるプログラム」を効率よく組もうと、
与えられた条件で最も少ない試行回数を出そうと挑んだのですが、どのような考え方でコードを組めばよいか思いつかなくて、調べてもうまく見つけられなかったので質問させていただきました。

＜例＞
例えば、
[0,1,2,3,4]から[2,3,1,4,0]という形を目指すとします。
その際、与えられた"特定のパターン"として
１．[2,3,0,1,4]
２．[4,2,3,1,0]があり、
（１・２はそれぞれ、移動前の[0,1,2,3,4]の同じ値の要素の移り先を表しています）
１を２回したとすると、
[0,1,2,3,4]→[2,3,0,1,4]→[0,1,2,3,4]　となる、といった具合です。

特定のパターンは１～３つまでで、その都度ランダムに生成させます。
幾らやっても成り立たないケースはFalseで返す予定です。

なにか良い案がありましたら、ご教授ください。よろしくお願い致します。

Answer 1

幾らやっても成り立たないケースはFalseで返す予定です。

いくらやっても成り立たない場合はありません。

与えられた条件で最も少ない試行回数を出そうと挑んだのですが、どのような考え方でコードを組めばよいか思いつかなくて、調べてもうまく見つけられなかったので質問させていただきました。

ある順列から別の順列への変換は数学でいう「置換」と考えることができます。
置換は必ず互換の積で表すことができる [1] ので、その互換の積を求めることができれば、それで swap パターンを求められたことになります。

【行列式編】互換の求め方と置換の符号 | 大学1年生もバッチリ分かる線形代数入門
【行列式編】置換と巡回置換 | 大学1年生もバッチリ分かる線形代数入門

上記の内容を踏まえた上でアルゴリズムを考えると、以下のようになります。

サンプルコード

順列を置換の積で表す。

def cyclic_form(permutation):
    cycles = []  # 置換の一覧

    unvisited = permutation.copy()
    while unvisited:
        j = i = unvisited.pop()
        cycle = [i]  # 起点を追加する。
        while True:
            j = permutation[j]  # 1つ移動する。
            if j == i:
                break  # 起点に戻ってきたら一巡したことになるので、break
            cycle.append(j)
            unvisited.remove(j)  # 1度調べた点は除く。
        cycles.append(cycle)

    return cycles

置換を互換の積に分解する。

def transpositions(cycles):
    trans = []
    for c in cycles:
        cycle_len = len(c)
        if cycle_len == 2:
            # 置換の長さが2ならすなわち互換
            trans.append(tuple(c))
        elif cycle_len > 2:
            # 長さ3以上の場合は、末尾から順に互換に分解する。
            first = c[0]
            for x in c[cycle_len - 1:0:-1]:
                trans.append((first, x))
    return trans

結果を出力する。

def print_show(N, transpositions):
    lst = list(range(N))
    # 結果を表示する。
    for i, j in transpositions:
        lst[i], lst[j] = lst[j], lst[i]  # 交換する。
        print('swap({}, {}): {}'.format(i, j, lst))  # 交換後の順列を表示する。
    print('number of swaps:', len(transpositions))  

dst = [2, 3, 1, 4, 0]  # スワップ後

cycles = cyclic_form(dst)
print(cycles)  # [[0, 2, 1, 3, 4]]

trans = transpositions(cycles)
print(trans)  # [(0, 4), (0, 3), (0, 1), (0, 2)]

print_show(len(dst), trans)
# swap(0, 4): [4, 1, 2, 3, 0]
# swap(0, 3): [3, 1, 2, 4, 0]
# swap(0, 1): [1, 3, 2, 4, 0]
# swap(0, 2): [2, 3, 1, 4, 0]
# number of swaps: 4

sympy を使う場合

sympy に順列を扱うモジュールがあるので、自前で実装した上記のことは以下のようにかけます。
Permutations — SymPy 1.4 documentation

from sympy.combinatorics import Permutation

dst = [2, 3, 1, 4, 0]

p = Permutation(dst)  # 置換
cycles = p.transpositions()  # 置換を互換の積に分解する。

print_show(len(dst), trans)
# swap(0, 4): [4, 1, 2, 3, 0]
# swap(0, 3): [3, 1, 2, 4, 0]
# swap(0, 1): [1, 3, 2, 4, 0]
# swap(0, 2): [2, 3, 1, 4, 0]
# number of swaps: 4

引用

[1] Cyclic permutation - Wikipedia
[2] 【行列式編】互換の求め方と置換の符号 | 大学1年生もバッチリ分かる線形代数入門
[3] 【行列式編】置換と巡回置換 | 大学1年生もバッチリ分かる線形代数入門

追記

質問内容を勘違いしていたため、追記。

---

課題

• 長さ N の最初の並び順と目標の並び順、すべての要素を同時に並び替えるパターンがランダムに1～3個与えられる。
• 与えられたパターンの並び替えを繰り返すことで、目標の並び順にする最小の組み合わせを考える。
• そのような組み合わせが見つからない場合は False を返す。

考え方

例として、N=3 の場合を考えます。

最初の並び順 [0, 1, 2]
目標の並び順 [2, 1, 0]
並び変えパターン [1, 0, 2], [0, 2, 1]

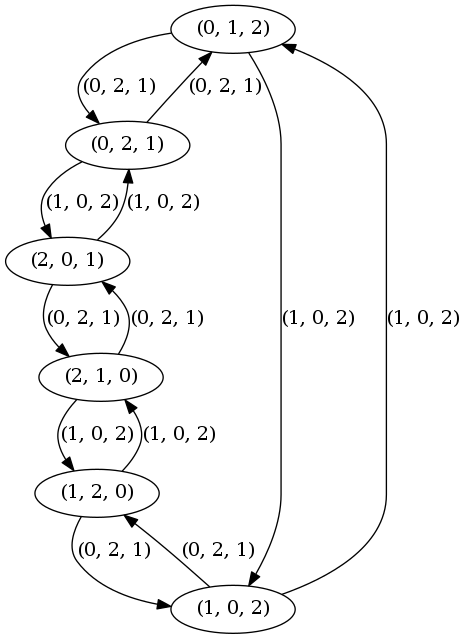
このとき、最初の並び順 [0, 1, 2] を起点として、与えられたパターンで並び変えを深さ優先探索で行っていくことで、以下のようなグラフが作れます。(数学的には置換群の ケイリーグラフ というそうです。)

点は並び順、辺は実行した並び替えのパターンを意味します。
例えば、並び順 (0, 2, 1) に対して、並び替え (1, 0, 2) を実行すると、並び順は (2, 0, 1) になりますので、点 (0, 2, 1) から点 (2, 0, 1) に対して、(1, 0, 2) というラベルのついた辺があります。
長さ3の並び順は3!=6なので、最大で6個の点ができます。

この時点で、目標の並び順の点が存在しない場合、どんなに並び替えを繰り返しても目標の順番にはならないということを意味するので、False を返すようにします。

最小の並び替え実行パターンを考えるには、グラフにおいて点 [0, 1, 2] から点 [2, 1, 0] に至る長さが最小の道を見つければよいことになります。

答えは以下の2つ

(0, 2, 1) (1, 0, 2) (0, 2, 1) 
(1, 0, 2) (0, 2, 1) (1, 0, 2)

ある点からある点へ至る最短ルートの算出は、すべての辺の重みを1にしたダイクストラ法で求められます。

まとめると、

1. 最初の並び順から与えられた1 ~ 3 個の並び替えを深さ優先探索で実行して、グラフを作成する。
2. 目標の並び順を表す点がグラフに存在しない場合は False を返す。
3. 最初の並び順から目標の並び順に至る長さ最小の道をダイクストラ法で見つける。

Comments

[Tetron]

ご回答有難うございます。
数学がニガテなので調べつつ解読させていただいたのですが、上記のサンプルコードは"[0,1,2,3,4]の状態から指定した順序までの置き換えにかかる二項間での入れ替え回数"を出力する認識で宜しいでしょうか。

＜例＞内の１．２．にも記した通り、私が想定しているものは指定した順序まで「指定した入れ替え方」で行うので、ただ闇雲に「互換」を行った場合の最小回数ではないです。
互換の積の分解で、
[0,1,2,3,4]から１．の[2,3,0,1,4]の状態になってから目標の[2,3,1,4,0]になるわけでもなく、
その与えられた順序[2,3,0,1,4]の並びに、５つまとめて動く必要があります。
この５つ同時に動く一つの処理で、何回かかるかという処理についての質問です。

求めていた回答とは異なりましたが、参考にさせていただきます。ありがとうございます。
加え、拙い質問文で誤解を招いてしまいました、すみません。
宜しければまたの回答、お待ちしております。

[tiitoi]

申し訳ありません。質問の課題内容を勘違いしておりました。
回答の内容は目標の順序にするための2要素間のスワップ方法及び回数の一例を出力する方法になります。

そうではなく、5個同時に並び替える与えられた複数のパターンを使って、目的の並び順にするにはそれらをどのように組み合わせるのがよいかという問題ですね。
やり方を考えてみましたが、入れ替えを実行する最大試行回数を決めて、全探索で組み合わせを探すぐらいしか思いつかないですね。(試行回数内で見つからなかったら False)

[tiitoi]

おそらく、本質的なやり方を思いついたので、追記しました。

Answer 2

編集距離、動的計画法などで検索すると良いかもしれません。

Comments

[Tetron]

回答ありがとうございます。
どのように検索すればよいかわからなかったので、とても助かります。