前提・実現したいこと
C言語を学習している者です。
sin波を合成すると振幅1の矩形波に近づくことが知られています。

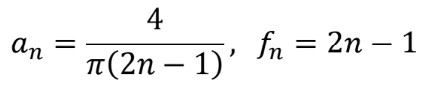

そこで、N個のsin波を合成したものと振幅1の矩形波との近似精度を相関係数で求めるプログラムを作成しました(以下)。
※範囲は0~1[s]で0.001[s]刻みのプロット値1000個をもとに相関係数を算出。
※Nは1~10, 100, 1000, 10000と実行するごとに変更する。
本来は、Nが大きくなるごとに、N個のsin波を合成したものは矩形波に近づく、つまり相関係数の絶対値は1に近づくのですが、次のような誤った結果が出てしまいます。
N 相関係数 1 0.901215 2 0.300397 3 0.180229 4 0.128725 5 0.100109 6 0.081896 7 0.069286 8 0.060037 9 0.052962 10 0.047376 100 0.003923 1000 0.901215 10000 0.901215
何が原因で誤った結果が出ているのか分からずに悩んでいます。
初心者なので分かりやすく教えて頂けると幸いです。
発生している問題・エラーメッセージ
Nが大きくなるほど相関係数の大きさが1に近づくはずなのに、正しい結果がファイルに出力されない。 エラーは出ていない。
該当のソースコード
C
1#define _USE_MATH_DEFINES 2#define N 10000 //1~10, 100, 1000, 10000と実行するごとに変更 3#include<stdio.h> 4#include<math.h> 5void RectangularInput(double *y){ 6 int i; 7 y[0] = 0.0; 8 for(i=1; i<500; i++) y[i] = 1.0; 9 y[500] = 0.0; 10 for(i=501; i<1000; i++) y[i] = -1.0; 11} 12double Average(int len, double *a){ 13 double mean = 0.0; 14 for(int i=0; i<len; i++) mean += a[i]; 15 mean /= (double)len; 16 return mean; 17} 18double Correlation(int len, double *x, double *y){ 19 int i; 20 double xave = Average(len, x); 21 double yave = Average(len, y); 22 double sx=0.0, sy=0.0, sxy=0.0; 23 for(i=0; i<len; i++) sx += pow(x[i]-xave, 2); 24 sx = sqrt(sx); 25 for(i=0; i<len; i++) sy += pow(y[i]-yave, 2); 26 sy = sqrt(sy); 27 for(i=0; i<len; i++) sxy += (x[i]-xave) * (y[i]-yave); 28 return sxy/(sx*sy); 29} 30int main(){ 31 FILE *fp = fopen("20266005_accuracy.txt", "a+"); 32 int i, n, len=1000; 33 double x[1000], y[1000], t, f, a, delta=1.0e-3; 34 for(i=0; i<len; i++){ 35 t = (double)i*delta; 36 for(n=1; n<=N; n++){ 37 f = 2*n-1; 38 a = 4/(M_PI*(2*n-1)); 39 x[i] = a * sin(2.0*M_PI*f*t); 40 } 41 } 42 RectangularInput(y); 43 fprintf(fp, "%d %lf\n", N, Correlation(len, x, y)); 44 fclose(fp); 45 return 0; 46} 47
補足情報(FW/ツールのバージョンなど)
Visual Studio Codeを使用してコードを記述。
gccでコンパイル。
回答1件
あなたの回答
tips
プレビュー






