「Jupiter notebook」にて、分布図の確認を行っていたのですが、確率密度?の見方が分からなかったため、質問させてもらいました。
以下はデータの一覧(5つのレコードまで)です。

こちらのヒストグラムの見方ですが、横軸がデータ(値)であるとの認識でおります。
その場合、「0.3 ~ 0.4」の範囲で、縦軸の数値「1」が対応しているかと思うのですが、この「1」は何を示しているのでしょうか...?
縦軸は確率密度らしいのですが、いまいち確率密度というのが分からなかった為、どなたかアドバイス頂けますと幸いです。
よろしくお願いします。
追記です
気になる質問をクリップする
クリップした質問は、後からいつでもMYページで確認できます。
またクリップした質問に回答があった際、通知やメールを受け取ることができます。
バッドをするには、ログインかつ
こちらの条件を満たす必要があります。
回答2件
0
ベストアンサー
グラフの見方について
青のバーと青の折れ線は分けて考えてください。
- 青のバー: データから作成したヒストグラムです。
- 青の折れ線: データの母集団分布をカーネル密度推定 (kernel density estimation, KDE) という手法で推定した確率密度関数を描画したものです。
seaborn.distplot の kde=True (デフォルト) の場合に、ヒストグラムの他にこのグラフが描画されます。
実装上は statsmodels がインストールされている場合は statsmodels.nonparametric.kde.KDEUnivariate、そうでない場合は scipy.stats.gaussian_kde に処理を投げるようになっています。
確率密度関数について
連続型の確率変数 X があるとき、X がある値 a 以下をとる確率を P(X <= a) としたとき、
で定義される f(x) が確率密度関数です。
※ 確率変数 = とり得る値が確率によって決まる変数。例えば、X をサイコロの目としたとき、X = 1 (1の目) は、1/ 6 の確率で出る。
注意したいのは、f(c) の値は、X = c となる確率ではありません。
X = c となる確率 P(X = c) は定義に従って計算すると、0 になります。
確率密度関数の見方としては、確率密度関数 f(x) の値が大きいところは、そのあたりの x の値が現れる可能性が高いという理解でいいと思います。
体系的に理解したい場合は 統計学 の教科書を当たると、最初のほうで必ず紹介されていると思うので、それを参照してください。
追記
ストーリーとしては、以下のようになります。
いくつかのデータが得られた
↓
データが得られた背景となる確率分布があるけど、それはわからない
↓
データから確率分布を推定する
統計学の考え方としては、まずなんらかの真の確率分布があり (現実ではこれはわからない)、データはその確率分布から得られた標本 (値の例) であると考えます。
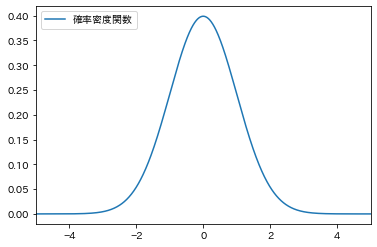
以下、例として、標準正規分布としておきます。
python
1from scipy.stats import norm, gaussian_kde 2import numpy as np 3import matplotlib.pyplot as plt 4 5# 平均0、分散1の1変量正規分布に従う確率変数 6rv = norm(loc=0, scale=1) 7 8fig, ax = plt.subplots() 9ax.plot(xs, rv.pdf(xs), label="確率密度関数") 10ax.legend(loc="upper left") 11ax.set_xlim(-5, 5) 12plt.show()
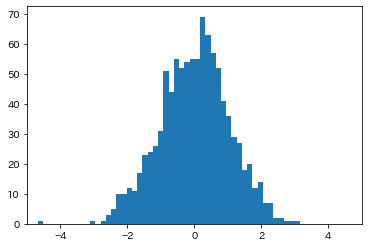
このような分布があって、そこから1000 個の値が得られたとします。
ヒストグラムを描画すると以下のようになります。
現実では、いくつかのデータが得られたとして、真の確率分布というのはわからないわけです。
例えば、100人に身長を聞いて、[168, 172, 180, ...] と100人分のデータが得られたとして、その元となった真の確率分布というのはわかりません。
わからないので、それを今持っているデータから推定するというのが、統計学の1つの目的になります。
カーネル密度推定はその手法の1つです。
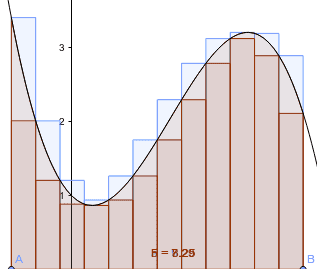
カーネル密度推定を使って推定すると、以下のようになります。
元の分布 (青) がわからなくても、データからある程度それに近い分布 (オレンジ) が得られました。
python
1# この得られた標本から元となる確率密度関数を推定する。 2kernel = gaussian_kde(samples) 3 4# 確率密度関数を描画する。 5xs = np.linspace(-5, 5, 1000) 6 7fig, ax = plt.subplots() 8ax.plot(xs, rv.pdf(xs), label="確率密度関数") 9ax.plot(xs, kernel(xs), label="推定した確率密度関数") 10ax.legend(loc="upper left") 11ax.set_xlim(-5, 5) 12plt.show()
追記
2つのグラフで「y」の値が、一方は少数、一方は整数となっておりますが、これは何故かがわかりません。
グラフの目盛りがすべて整数なら整数、小数が含まれるなら小数で表示するという matplotlib の仕様によるものなので、整数か小数かはグラフの表示上の問題であり、重要ではありません。
注目するべきは、y 軸のスケールが左と右で大きく違うことでしょう。
これは、他の回答者様のコメント欄で hayataka2049 さんがご指摘されていますが、ヒストグラムの正規化 (デフォルトで有効) によるものです。
通常、ヒストグラムは y 軸は各ビンに属するデータ数 (頻度値) ですが、この正規化が有効の場合、棒の面積の合計が1となるように棒の高さが調整されます。
数式で表すと、n 個のビンの幅が w1, w2, ..., wn、頻度値が f1, f2, ..., fn としたとき、
w1 * f1 + w2 * f2 + ... + wn + fn = 1
となるように f1, f2, ..., fn の値を正規化します。
左のほうが右より棒の高さが高いのは、左の方はビンの幅が小さいので、棒の面積の合計が1にするためには棒の高さをその分高くする必要があるからです。
棒の高さをそのビンに属するデータ数として解釈したい場合は distplot() で norm_hist=False を指定してください。
この正規化の仕様は、内部でヒストグラム作成に使用している numpy.histogram から来ています。
また、can110さんのご回答で、「描かれた曲線とx軸とを囲む領域の面積がデータ値の出現個数の総数になるように補正、正規化された値だということのようです。」とあるのですが、
仮に左側の画像の総面積を求めてみますと、x軸が「0.0 ~ 0.3」の為、「0.3」y軸を大体ではありますが「6」と考えた場合、「0.3 × 6 ÷ 2」 = 「0.9」となります。
こちらのデータ値の出現個数の総数が「0.9」であるという意味がいまいち分からない為、ご助言頂けましたら幸いです...
曲線のほうは、先の回答の通り、推定した確率密度関数です。
「描かれた曲線とx軸とを囲む領域の面積」とは、確率密度関数を (-∞, +∞) の区間で積分すると求められ、これは1になります。
この計算の解釈は、確率変数 X は実数の値をとるので、(-∞, +∞) の間の値をとる確率は100%であるということを言っています。
補足
正規化されたヒストグラム、カーネル密度推定で推定した確率密度関数ですが、どちらも(不明な)真の確率密度関数を近似するのが目的です。
曲線とx軸の間の面積を求めるのに、x 軸を細かい区間で分割して、長方形を敷き詰めて、面積を計算するというのが、リーマン積分の考え方です。
なので、大量のデータを用意して、ビンの幅を小さくした正規化されたヒストグラムを作成すれば、それで真の確率密度関数を近似できます。
python
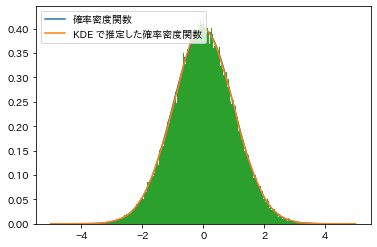
1from scipy.stats import norm, gaussian_kde 2import numpy as np 3import matplotlib.pyplot as plt 4 5# 平均0、分散1の1変量正規分布に従う確率変数 6rv = norm(loc=0, scale=1) 7 8# 大量の標本を生成する。 9samples = rv.rvs(300000) 10 11# この得られた標本から元となる確率密度関数を推定する。 12kernel = gaussian_kde(samples) 13 14fig, ax = plt.subplots() 15 16# 確率密度関数を描画する。 17xs = np.linspace(-5, 5, 1000) 18ax.plot(xs, rv.pdf(xs), label="確率密度関数") 19ax.plot(xs, kernel(xs), label="KDE で推定した確率密度関数") 20 21# ヒストグラムを描画する。 22bins = np.linspace(-5, 5, 1000) 23ax.hist(samples, bins, density=True) 24ax.legend(loc="upper left") 25plt.show()
「カーネル密度推定の確率密度関数 (オレンジ)」は「真の確率密度関数」と一致して重なっている。
「正規化されたヒストグラム(緑)」も「真の確率密度関数」とほぼ一致している。
追記 distplot の仕様確認
引数の優先度としては、norm_hist < kde < hist_kws のようですので、
正規化したくない場合は、kde=False または hist_kws={"density": False} を指定するのがよさそうです。
| kde | density | ヒストグラム |
|---|---|---|
| False | False | 正規化されない |
| False | True | 正規化される |
| True | False | 正規化されない |
| True | True | 正規化される |
python
1import matplotlib.pyplot as plt 2import numpy as np 3import seaborn as sns 4 5sns.set() 6np.random.seed(0) 7 8x = np.random.randn(1000) 9 10fig, axes = plt.subplots(2, 2, figsize=(8, 8)) 11axes = axes.ravel() 12 13axes[0].set_title("kde=False, density=False") 14sns.distplot(x, kde=False, hist_kws={"density": False}, ax=axes[0]) 15axes[1].set_title("kde=False, density=True") 16sns.distplot(x, kde=False, hist_kws={"density": True}, ax=axes[1]) 17axes[2].set_title("kde=True, density=False") 18sns.distplot(x, kde=True, hist_kws={"density": False}, ax=axes[2]) 19axes[3].set_title("kde=True, density=True") 20sns.distplot(x, kde=True, hist_kws={"density": True}, ax=axes[3]) 21plt.show()
| kde | norm_hist | ヒストグラム |
|---|---|---|
| False | False | 正規化されない |
| False | True | 正規化される |
| True | False | 正規化される |
| True | True | 正規化される |
import matplotlib.pyplot as plt import numpy as np import seaborn as sns sns.set() np.random.seed(0) x = np.random.randn(1000) fig, axes = plt.subplots(2, 2, figsize=(8, 8)) axes = axes.ravel() axes[0].set_title("kde=False, norm_hist=False") sns.distplot(x, kde=False, norm_hist=False, ax=axes[0]) axes[1].set_title("kde=False, norm_hist=True") sns.distplot(x, kde=False, norm_hist=True, ax=axes[1]) axes[2].set_title("kde=True, norm_hist=False") sns.distplot(x, kde=True, norm_hist=False, ax=axes[2]) axes[3].set_title("kde=True, norm_hist=True") sns.distplot(x, kde=True, norm_hist=True, ax=axes[3]) plt.show()
投稿2020/02/09 10:54
編集2020/02/11 07:19総合スコア21956
0
What is y axis in seaborn distplot?にてほぼそのままの質問と回答がありましたので、まずは一読ください。
正直「確率密度」とは何かなどがいまいちほぼほぼ理解できていないのですが、Prasann Barotさんの回答をgoogle翻訳した結果を引用します。
ANS->密度プロットのy軸は、カーネル密度推定の確率密度関数です。ただし、これは確率ではなく確率密度であると指定するように注意する必要があります。違いは、確率密度とは、x軸上の単位あたりの確率です。実際の確率に変換するには、x軸上の特定の間隔の曲線の下の領域を見つける必要があります。やや紛らわしいことに、これは確率ではなく確率密度であるため、y軸は1より大きい値を取ることができます。
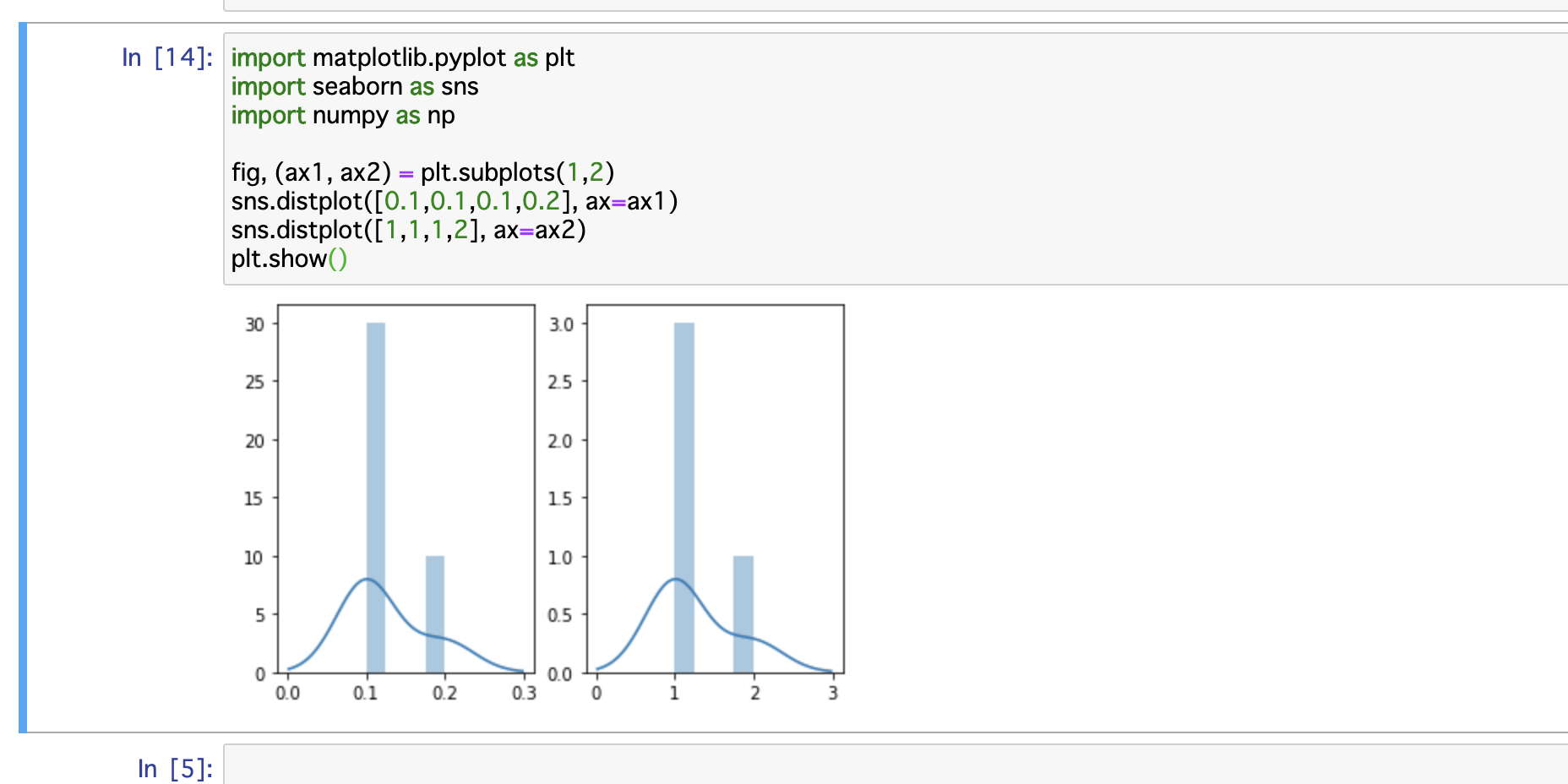
つまりy軸は確率密度を示す値ですが、描かれた曲線とx軸とを囲む領域の面積がデータ値の出現個数の総数になるように補正、正規化された値だということのようです。
これは以下のようなコードにて簡単な図を描くことで確かめられます。
以下の図において右側はx値が左側の10倍であるためy軸の値は1/10になっています。
またざっと目視で曲線とx軸で囲まれた領域の面積を求めてみます。
どちらも約1.25となり、実際の出現個数の総数4と、少し離れた値になっていますが、これは推定の仕方、distplotでデフォルトで使用している確率密度関数の性質に起因するものです。
python
1import matplotlib.pyplot as plt 2import seaborn as sns 3import numpy as np 4 5print(sns.__version__) # 0.9.0 6 7fig, (ax1, ax2) = plt.subplots(1,2) 8sns.distplot([0.1,0.1,0.1,0.2], ax=ax1) 9sns.distplot([1,1,1,2], ax=ax2) 10plt.show()
曲線の意味
この図の曲線(確率密度関数)を用いると、与えられたデータ群以外のデータ値の出現確率(個数)を推定することができます。
たとえば左側の図においてx=0.075というデータ値の出現確率(個数)は以下によって求めることができます。
今x値から上に直線を伸ばして曲線とそれに交わった点のy軸の値を見ます。この場合は約10になります。
これにx=0.075を掛けて0.75個という値がx=0.075の出現確率(個数)となります。
ただ、直感的にはもう少し大きな値になるのが自然そうで、あまり当てにならない感じもします。
ということでPrasann Barotさんの回答の続き
密度プロットの唯一の要件は、曲線下の総面積が1つに統合されることです。私は一般に、密度プロットのy軸を、異なるカテゴリ間の相対的な比較の値としてのみ考える傾向があります。
という回答になっているのかと思います。
投稿2020/02/08 12:41
編集2020/02/09 05:07総合スコア38266
バッドをするには、ログインかつ
こちらの条件を満たす必要があります。
2020/02/09 06:18 編集
2020/02/10 01:56 編集
あなたの回答
tips
太字
斜体
打ち消し線
見出し
引用テキストの挿入
コードの挿入
リンクの挿入
リストの挿入
番号リストの挿入
表の挿入
水平線の挿入
プレビュー
質問の解決につながる回答をしましょう。 サンプルコードなど、より具体的な説明があると質問者の理解の助けになります。 また、読む側のことを考えた、分かりやすい文章を心がけましょう。












バッドをするには、ログインかつ
こちらの条件を満たす必要があります。
2020/02/09 11:29 編集
2020/02/09 12:22 編集
2020/02/09 13:36 編集
2020/02/09 14:10
2020/02/10 00:26
2020/02/10 15:59 編集
2020/02/10 22:52
2020/02/11 02:30 編集
2020/02/11 02:38
2020/02/11 07:26 編集
2020/02/11 08:31