今あるプログラムは“x”と“y”の項があるため,原点を通らない近似となってしまいます.
近似式を
ax^2+bxy+cy^2=1
となるようにしたいです.
以下にプログラムを載せておきます.
わかるかたおねがいします.
入力データは【data.txt】の列を読み取るようになっています.
お願いします.
Python
1import numpy 2import matplotlib.pyplot as plt 3from matplotlib.patches import Ellipse 4 5"""Demonstration of least-squares fitting of ellipses 6 __author__ = "Ben Hammel, Nick Sullivan-Molina" 7 __credits__ = ["Ben Hammel", "Nick Sullivan-Molina"] 8 __maintainer__ = "Ben Hammel" 9 __email__ = "bdhammel@gmail.com" 10 __status__ = "Development" 11 Requirements 12 ------------ 13 Python 2.X or 3.X 14 numpy 15 matplotlib 16 References 17 ---------- 18 (*) Halir, R., Flusser, J.: 'Numerically Stable Direct Least Squares 19 Fitting of Ellipses' 20 (**) http://mathworld.wolfram.com/Ellipse.html 21 (***) White, A. McHale, B. 'Faraday rotation data analysis with least-squares 22 elliptical fitting' 23""" 24 25class LSqEllipse: 26 27 def fit(self, data): 28 """Lest Squares fitting algorithm 29 Theory taken from (*) 30 Solving equation Sa=lCa. with a = |a b c d f g> and a1 = |a b c> 31 a2 = |d f g> 32 Args 33 ---- 34 data (list:list:float): list of two lists containing the x and y data of the 35 ellipse. of the form [[x1, x2, ..., xi],[y1, y2, ..., yi]] 36 Returns 37 ------ 38 coef (list): list of the coefficients describing an ellipse 39 [a,b,c,d,f,g] corresponding to ax**2+2bxy+cy**2+2dx+2fy+g 40 """ 41 x, y = numpy.asarray(data, dtype=float) 42 43 #Quadratic part of design matrix [eqn. 15] from (*) 44 D1 = numpy.mat(numpy.vstack([x**2, x*y, y**2])).T 45 #Linear part of design matrix [eqn. 16] from (*) 46 D2 = numpy.mat(numpy.vstack([x, y, numpy.ones(len(x))])).T 47 48 #forming scatter matrix [eqn. 17] from (*) 49 S1 = D1.T*D1 50 S2 = D1.T*D2 51 S3 = D2.T*D2 52 53 #Constraint matrix [eqn. 18] 54 C1 = numpy.mat('0. 0. 2.; 0. -1. 0.; 2. 0. 0.') 55 56 #Reduced scatter matrix [eqn. 29] 57 M=C1.I*(S1-S2*S3.I*S2.T) 58 59 #M*|a b c >=l|a b c >. Find eigenvalues and eigenvectors from this equation [eqn. 28] 60 eval, evec = numpy.linalg.eig(M) 61 62 # eigenvector must meet constraint 4ac - b^2 to be valid. 63 cond = 4*numpy.multiply(evec[0, :], evec[2, :]) - numpy.power(evec[1, :], 2) 64 a1 = evec[:, numpy.nonzero(cond.A > 0)[1]] 65 66 #|d f g> = -S3^(-1)*S2^(T)*|a b c> [eqn. 24] 67 a2 = -S3.I*S2.T*a1 68 69 # eigenvectors |a b c d f g> 70 self.coef = numpy.vstack([a1, a2]) 71 self._save_parameters() 72 73 def _save_parameters(self): 74 """finds the important parameters of the fitted ellipse 75 76 Theory taken form http://mathworld.wolfram 77 Args 78 ----- 79 coef (list): list of the coefficients describing an ellipse 80 [a,b,c,d,f,g] corresponding to ax**2+2bxy+cy**2+2dx+2fy+g 81 Returns 82 _______ 83 center (List): of the form [x0, y0] 84 width (float): major axis 85 height (float): minor axis 86 phi (float): rotation of major axis form the x-axis in radians 87 """ 88 89 #eigenvectors are the coefficients of an ellipse in general form 90 #a*x^2 + 2*b*x*y + c*y^2 + 2*d*x + 2*f*y + g = 0 [eqn. 15) from (**) or (***) 91 a = self.coef[0,0] 92 b = self.coef[1,0]/2. 93 c = self.coef[2,0] 94 d = self.coef[3,0]/2. 95 f = self.coef[4,0]/2. 96 g = self.coef[5,0] 97 98 #finding center of ellipse [eqn.19 and 20] from (**) 99 x0 = (c*d-b*f)/(b**2.-a*c) 100 y0 = (a*f-b*d)/(b**2.-a*c) 101 102 #Find the semi-axes lengths [eqn. 21 and 22] from (**) 103 numerator = 2*(a*f*f+c*d*d+g*b*b-2*b*d*f-a*c*g) 104 denominator1 = (b*b-a*c)*( (c-a)*numpy.sqrt(1+4*b*b/((a-c)*(a-c)))-(c+a)) 105 denominator2 = (b*b-a*c)*( (a-c)*numpy.sqrt(1+4*b*b/((a-c)*(a-c)))-(c+a)) 106 width = numpy.sqrt(numerator/denominator1) 107 height = numpy.sqrt(numerator/denominator2) 108 109 # angle of counterclockwise rotation of major-axis of ellipse to x-axis [eqn. 23] from (**) 110 # or [eqn. 26] from (***). 111 phi = .5*numpy.arctan((2.*b)/(a-c)) 112 113 self._center = [x0, y0] 114 self._width = width 115 self._height = height 116 self._phi = phi 117 118 @property 119 def center(self): 120 return self._center 121 122 @property 123 def width(self): 124 return self._width 125 126 @property 127 def height(self): 128 return self._height 129 130 @property 131 def phi(self): 132 """angle of counterclockwise rotation of major-axis of ellipse to x-axis 133 [eqn. 23] from (**) 134 """ 135 return self._phi 136 137 def parameters(self): 138 return self.center, self.width, self.height, self.phi 139 140 141def make_test_ellipse(center=[1,1], width=1, height=.6, phi=3.14/5): 142 """Generate Elliptical data with noise 143 144 Args 145 ---- 146 center (list:float): (<x_location>, <y_location>) 147 width (float): semimajor axis. Horizontal dimension of the ellipse (**) 148 height (float): semiminor axis. Vertical dimension of the ellipse (**) 149 phi (float:radians): tilt of the ellipse, the angle the semimajor axis 150 makes with the x-axis 151 Returns 152 ------- 153 data (list:list:float): list of two lists containing the x and y data of the 154 ellipse. of the form [[x1, x2, ..., xi],[y1, y2, ..., yi]] 155 """ 156 t = numpy.linspace(0, 2*numpy.pi, 1000) 157 x_noise, y_noise = numpy.random.rand(2, len(t)) 158 159 ellipse_x = center[0] + width*numpy.cos(t)*numpy.cos(phi)-height*numpy.sin(t)*numpy.sin(phi) + x_noise/2. 160 ellipse_y = center[1] + width*numpy.cos(t)*numpy.sin(phi)+height*numpy.sin(t)*numpy.cos(phi) + y_noise/2. 161 162 return [ellipse_x, ellipse_y]
Python
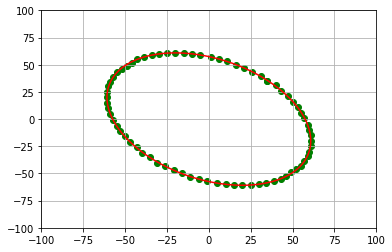
1import numpy as np 2import matplotlib.pyplot as plt 3import ellipses as el 4from matplotlib.patches import Ellipse 5 6alpha = 5 7beta = 3 8N = 500 9DIM = 2 10 11fig = plt.figure(1) 12ax = fig.add_subplot(111) 13 14 15 16 17np.random.seed(2) 18 19# Generate random points on the unit circle by sampling uniform angles 20theta = np.random.uniform(0, 2*np.pi, (N,1)) 21eps_noise = 0.2 * np.random.normal(size=[N,1]) 22circle = np.hstack([np.cos(theta), np.sin(theta)]) 23 24# Stretch and rotate circle to an ellipse with random linear tranformation 25B = np.random.randint(-3, 3, (DIM, DIM)) 26noisy_ellipse = np.loadtxt("data.txt") 27 28# Extract x coords and y coords of the ellipse as column vectors 29X = noisy_ellipse[:,0:1] 30Y = noisy_ellipse[:,1:] 31 32# Formulate and solve the least squares problem ||Ax - b ||^2 33A = np.hstack([X**2, X * Y, Y**2, X, Y]) 34b = np.ones_like(X) 35x = np.linalg.lstsq(A, b)[0].squeeze() 36 37# Print the equation of the ellipse in standard form 38print('The ellipse is given by {0:.3}x^2 + {1:.3}xy+{2:.3}y^2+{3:.3}x+{4:.3}y = 1'.format(x[0], x[1],x[2],x[3],x[4])) 39 40# Plot the noisy data 41plt.scatter(X, Y, label='Data Points', color='g')
回答1件
あなたの回答
tips
プレビュー





バッドをするには、ログインかつ
こちらの条件を満たす必要があります。
退会済みユーザー
2020/01/22 07:55
2020/01/22 12:12
退会済みユーザー
2020/01/22 13:15