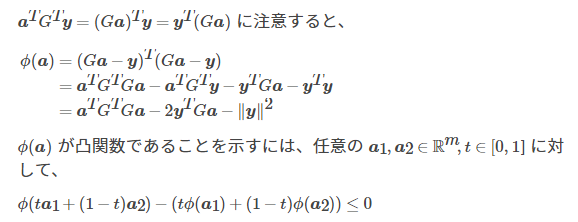勾配法で局所解が発生するときの次数は4以上か？

Question

機械学習で例えば回帰を行うとします。
回帰曲線が非線形の場合では勾配法を用いますが、勾配法で局所解が生じる場合の回帰曲線の形が知りたいです。
回帰ではなく分類をする際の決定境界のﾓﾃﾞﾙを決めるときの勾配法での局所解のできる形もできれば知りたいですが
話が複雑そうになるのでまず回帰から行きたいと思います。

まず回帰曲線を

とし目的関数Eを

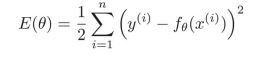
とします。
ここで勾配法の更新式は

ここで多項式回帰をするとし回帰曲線を

とします。多項式回帰の更新式は

となりますが
多項式回帰では図では次数が3次です。なので局所解は発生しませんが
次数が４次の場合の回帰曲線について

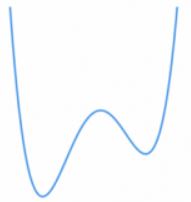
となるので次数が4次のﾊﾟﾗﾒｰﾀで目的関数Eを微分すると勾配法の解が局所解に陥ってしまう
この際確率的勾配法が有効なのかなと思いました。
あってますか？

Comments

[hayataka2049]

>回帰曲線が非線形の場合では勾配法を用いますが
とありますが、回帰曲線が次数2の多項式なら普通の（非線形ではない）最小二乗法を使い、正規方程式を解く方法でフィッティングできるのでは？

[ads3hcgff]

確かに次数２であれば線形であるので解析的に解くことができると思います。
勾配法を用いる必要性はないですね。今調べてみたところ３次４次でも解の公式があるらしく
次数４までは解析で解けるので勾配法を用いる必要はないんですかね？
ここで私が知りたいのは勾配法を使うと仮定して
真のﾊﾟﾗﾒｰﾀθ１θ２θ３・・・等を求める際どのような時に局所解ができるのかということです。
回帰曲線を３次関数の次数３のﾊﾟﾗﾒｰﾀで微分する際、勾配が真の解に向いてくれないということであっていますか？なので更新式で用いる一番最初のﾊﾟﾗﾒｰﾀを決める場合、次数３であれば最低でも二回はﾊﾟﾗﾒｰﾀを決めなおす必要があるということでしょうか

[hayataka2049]

別に回帰曲線が10次でも100次でも、パラメータで偏微分して連立一元方程式になれば行列で解けます。なので、もう少し複雑な問題を持ってこないと議論しづらい気がします。

Answer 1

解決済みですが、機械学習の立場からコメントします。
機械学習においてモデルパラメーターはコスト関数(質問記載します関数Eに相当)の最小化によって求められます。その際、機械学習ではこのコスト関数の形状はわからない(つまり、定式化できない)ことを前提にアプローチします。tiitoiさんが解説する最小二乗法とはこの点が明らかに異なります。
最小二乗法が解析的にパラメーターが求められるのに対し、機械学習は数値計算によって近似解を求めます。この数値計算ですが、大まかにいうと前回のパラメーターで求められたコスト関数の結果と今回の結果の差、今回のデータにおける微分値の正負、を基準にパラメーターの更新を繰り返してコスト関数の最小値を求めます。
よって、局所解が求められる条件は機械学習の立場からするとわからないということになると思います。

当然のことながら、コスト関数の形状が分からなければ、局所値と最小値の区別ができません。そこで、機械学習は確率的勾配法やミニバッチ学習などの方法が考案されました。これらは、先のパラメーター更新のルールである前回と今回の値の差に確率的な紛れを起こさせることで局所解の谷からジャンプさせるイメージです。
よって、質問の最後の部分は局所解回避という点であっていますが、コスト関数の形状不明が理由と考えるべきでしょう

Answer 2

理解が間違っていたらすみません。
teratail は数式入力できないので画像で失礼します。

---

最小二乗法の定式化

以下でいう最小二乗法の目的関数 J(a) は凸関数なので、局所解が大域解となるので、勾配法を使っても求まる解は大域解となるのではないでしょうか。

最小二乗法の目的関数が凸関数であることの証明

示すべきこと

J(a) が凸関数であることの証明は以下の不等式を示す必要があります。

式展開してゴリゴリ計算すれば導出できます。(わからなければ補足します。)

証明

画像はクリックすると拡大できます。

正規方程式

hayataka2049 さんがコメントしてくださった正規方程式との関係は以下のようになります。

Summary

• 最小二乗法の目的関数は凸関数
• 凸関数なので、局所解は大域解になる。
• なので、勾配法で解いても必ず大域解に収束する。
• 勾配法以外の方法として、正規方程式を解いても求められる。

追記

ここでいう線形、線形でないというのは、近似関数を推定するパラメータ a の関数として見たときの話です。

例えば、f(x) = a_1 x^4 + a_2 x^2 という関数で近似する場合、
x の関数としてみた場合非線形関数ですが、a の関数として見た場合線形関数です。
以下、損失関数を描画した例です。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import FancyArrowPatch
from mpl_toolkits.mplot3d import Axes3D, proj3d

xs = np.array([2.8, 2.9, 3.0, 3.1, 3.2, 3.2, 3.2, 3.3, 3.4])
ys = np.array([30, 26, 33, 31, 33, 35, 37, 36, 33])

# 近似関数 a1 x^4 + a2 x^2
def f1(a1, a2):
    return a1 * xs**4 + a2 * xs ** 2

# 近似関数 sin(a1) x^4 + a2 x^2
def f2(a1, a2):
    return np.sin(a1) * xs**4 + a2 * xs ** 2

# 2乗誤差関数
def loss(a1, a2, f):
    return ((ys - f(a1, a2)) ** 2).sum()

# 各点での関数 loss の値を計算する。
A1, A2 = np.mgrid[-10:11, -10:11]
L = np.array([loss(a1, a2, f2) for a1, a2 in zip(A1.ravel(), A2.ravel())])
L = L.reshape(A1.shape)

fig = plt.figure(figsize=(7, 7))
ax = fig.add_subplot(111, projection='3d')
# 各軸のラベルを設定する。
ax.set_xlabel('$a_1$', fontsize=15)
ax.set_ylabel('$a_2$', fontsize=15)
ax.set_zlabel('$loss$', fontsize=15)
# グラフを作成する。
ax.plot_surface(A1, A2, L, alpha=0.4, antialiased=False)
ax.view_init(elev=50, azim=120)

f(x) = a1 x^4 + a2 x^2 の2乗誤差関数
→ 凸なので局所解 = 大域解

f(x) = sin(a1) x^4 + a2 x^2 の2乗誤差関数
→ 局所解あり

Comments

[ads3hcgff]

回答ありがとうございます。
提示していただいた証明について細かいところは理解できていません。すいません。
なんとなく、多項式回帰でも、損失関数（目的関数）がE=1/2(y-t)^2になるので
下に凸の関数となり局所解が発生しないということを証明しているのかなと感じましたがあっているでしょうか・・・

[tiitoi]

最初に書いたのは、示すべきことで証明自体は書いてません。
編集して証明と hayataka2049 さんがコメントしていただいてる正規方程式の関係を追記しました。
よくわからなければ、とりあえず「最小二乗法で局所解の心配はしなくていい」と理解すればよいです。

[tiitoi]

上記の話をきちんと理解したい場合は
「これなら分かる最適化数学―基礎原理から計算手法まで」がおすすめです。
https://www.amazon.co.jp/dp/4320017862

[ads3hcgff]

証明の説明ありがとうございます。
早速その本を読んでみようと思います！
数学的知識があいまいなまま聞くのはすごい烏滸がましいのですが
１つだけすごい気になったので質問させてください。
>>「最小二乗法で局所解の心配はしなくていい」
損失関数が最小二乗法ではなく例えばクロスエントロピー誤差であれば
確率的勾配法を使う意味（局所解が発生）が出てくるということでしょうか。

[hayataka2049]

あれ、私としては目的関数 が凸関数になるのは「線形」最小二乗法の場合で、「非線形」最小二乗法の場合（というかそれに限らず非線形の最適化手法を持ってくる場合）は局所解もあり得るので、その点において質問者さんの問題意識そのものは正しい（ただし回帰曲線（回帰式の方が良いか）が非線形の場合、と勘違いしていて、そういう例を示している）と理解していました。そういうことですよね？

[tiitoi]

ads3hcgff さん
> クロスエントロピー誤差
クロスエントロピー誤差は通常クラス分類で使うものだと思っていたので、回帰で使えるのか、その場合凸関数になるのかちょっと自分もわからないです。すいません。

> hayataka2049さん
コメントありがとうごいます。
質問に挙げられてる例が ax + b, ax^2 + bx + c だったので、回答の (1) の線形結合で表せる関数を前提としていたのですが、たしかにご指摘いただいた通り、そうでない場合は二乗誤差が凸関数であることは保証されないです。

[tiitoi]

調べたら、線形結合で表せない関数で近似する場合も最小二乗法というのですね。その点を勘違いしてました。
https://ja.wikipedia.org/wiki/%E9%9D%9E%E7%B7%9A%E5%BD%A2%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%97%E6%B3%95

[ads3hcgff]

言葉足らずですいません
例えば
回帰曲線　f(x)=3x^4+2x^3+2x^2+x+2
があったとして
（ｼｸﾞﾏは省略してます。何個かﾃﾞｰﾀがあるとして）
最小二乗法
E=1/2(t-f(x))
=1/2(t-(3x^4+2x^3+2x^2+x+2))

を勾配法で更新するとき局所解は発生するでしょうか？
f(x)=3x^4+2x^3+2x^2+x+2は非線形関数でと思っていたのですが違うのでしょうか

[tiitoi]

> f(x)=3x^4+2x^3+2x^2+x+2は非線形関数

これは x の関数としてみたとき、非線形関数ですが、どれが推定対象のパラメータでしょうか。
f(x) = a_5 x^4 + a_4 x^3 + a_3 x^2 + a_2 x + a_1 の間違いですか？

[tiitoi]

損失関数を考えるときは、x を固定してパラメータ a の関数として考えるので、その場合、f(a) = a_5 x^4 + a_4 x^3 + a_3 x^2 + a_2 x + a_1 は線形関数ですよね。

[ads3hcgff]

f(x) = a_5 x^4 + a_4 x^3 + a_3 x^2 + a_2 x + a_1
ですすいません。
ﾊﾟﾗﾒｰﾀa_5とa_4とa_2について私の見解では
a_5が局所解 a_4は局所解は発生しないが真の解が求まらない場合がある
a_2については真の解が求まると思いました

[tiitoi]

おそらく質問者さんが疑問に思っている点は
f(x) = a_3 x^2 + a_2 x + a_1 のように非線形関数のとき、局所解に陥らないの？ということだと思いますが、
ここでいう線形、非線形というのは関数fを x を定数として aの関数として見た f(a_1, a_2, a_3) = a_3 x^2 + a_2 x + a_1 について言っています。
x^2, x は定数なので、この関数 f(a_1, a_2, a_3) が線形なのは明らかだと思います。

[tiitoi]

回答の議論が成り立つ: f(x) = a x + b
→ a, b の関数としてみると、線形

回答の議論が成り立たない: f(x) = a^2 x + b
→ a, b の関数としてみると、線形でない
→ 局所解に陥る可能性もある

なので、推定パラメータでない部分が x^4 とかでもそこは関係ありません。重要なのは近似関数がパラメータの線形結合として表されるかどうかです。

[ads3hcgff]

詳しく教えていただきありがとうございます！
じっくり考えてみます。

[tiitoi]

自分も認識不足の部分があり、当初、線形な場合の最小二乗法しか考えていなかったため、説明がわかりづらくなって申し訳ないです。
一応まとめておきます。

* 最小二乗法は線形、非線形にわけられる。
* このとき、線形、非線形というのは、推定パラメータに関して線形か非線形かを指す
→ 「線形、非線形とは何に対してのことか」この部分を理解するとこれまでの議論が見えてくると思います。↓同じ内容の質問
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11108629276
* 線形の場合は、回答の議論で局所解に陥ることはない
* 非線形の場合は、局所解に陥ることがある